Questões de Concurso
Filtrar
280 Questões de concurso encontradas
Página 20 de 56
Questões por página:
Questões por página:
Concurso:
Petrobras
Disciplina:
Não definido
Sendo f : ℜ 2 → ℜ definida por f ( x, y ) = x2 /x2 + y2 - x , o limite
f (x, y) existe e é igual a zero.
Ao se considerar ( x, y ) → ( 0,0 ) sobre as retas y = a.x ( a ∈ ℜ), obtém-se 
x2 /x2+ (ax)2-x= 0 , ∀ a ∈ ℜ.
Analisando-se as afirmações acima, conclui-se que
Concurso:
Petrobras
Disciplina:
Não definido
Uma transformação linear T : ℜ6 → ℜ5 , não nula, é tal que a dimensão de seu núcleo, Ker(T), é maior do que 4.
Diante de tais informações, conclui-se que a dimensão do conjunto imagem Im(T) é igual a
Diante de tais informações, conclui-se que a dimensão do conjunto imagem Im(T) é igual a
Concurso:
Petrobras
Disciplina:
Não definido
Se y(x) é a solução do problema de valor inicial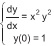 
qual é o valor de y(1)?
Concurso:
Petrobras
Disciplina:
Não definido
A função f : [0, + ∞ ) → ℜ é definida por f(t) = e2t sen (3t).
Se F(s)= 
e-st f(t) dt é a Transformada de Laplace da função f, então, para s > 2, F(s) é igual a
Concurso:
Petrobras
Disciplina:
Não definido
Seja f : [0, +∞) → ℜ uma função, seccionalmente contínua e de ordem exponencial, cuja Transformada de Laplace é F (s) =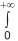 
e -st .f(t) dt = e-s/s2 para s > 0.
Dentre os gráficos abaixo, qual o que melhor se aproxima do gráfico da função f(t)?
