As informações abaixo foram extraídas de um quadro de análise de variância, cujo objetivo é testar a hipótese da igualdade das médias da variável X de 4 grupos I, II, III e IV, independentes, cada um contendo 8 observações.



O valor da estatística F (F calculado) utilizado para a verificação da igualdade das médias é

Um estudo tem como objetivo deduzir um modelo que permite encontrar uma relação linear, sem intercepto, entre duas variáveis X e Y com base em 20 observações. O modelo foi definido como Y_i = βX_i + ε_i , em que:

I. Y_i é uma variável aleatória e representa o valor da variável dependente na i-ésima observação.

II. X_i é o valor da variável explicativa na i-ésima observação.

III. ε_i é o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples.

IV. ß é o parâmetro do modelo, cuja estimativa foi obtida pelo método dos mínimos quadrados.



Utilizando a equação da reta encontrada pelo método dos mínimos quadrados, obtém-se que o valor de Y, quando X for igual a 50, é

Em uma cidade foi realizada uma pesquisa entre 600 eleitores, escolhidos aleatoriamente, com relação à preferência entre 2 candidatos X e Y para o cargo de prefeito. Esta pesquisa forneceu 2 grupos de eleitores, sendo 375 homens e 225 mulheres. Cada eleitor forneceu uma e somente uma resposta, na pesquisa, se preferia X ou Y.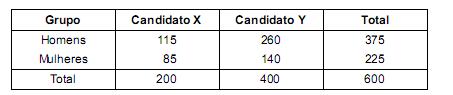



O objetivo é verificar, com relação a estes eleitores, se a preferência pelos candidatos depende do sexo, utilizando o teste qui-quadrado a um determinado nível de significância a.

Dados:

Valores críticos da distribuição qui-quadrado [P(qui-quadrado com n graus de liberdade)


É correto afirmar que

Durante 36 dias, observou-se, diariamente, a quantidade produzida de peças por duas máquinas de marcas M₁ e M₂, independentemente. Um fabricante verificou que subtraindo diariamente da quantidade de peças produzidas por M₁ a quantidade produzida por M₂ obteve a presença de sinal positivo nas diferenças de 20 produções e sinal negativo nas 16 restantes, não ocorrendo diferença nula. Aplicando o teste dos sinais para decidir se a proporção populacional de sinais positivos (p) é igual a 0,50, ao nível de significância de 5%, ele considerou as hipóteses H₀: p = 0,50 (hipótese nula) contra H₁: p ≠ 0,50 (hipótese alternativa). Com a aproximação da distribuição binomial pela normal sem a correção de continuidade, foi apurado o valor do escore r correspondente para comparação com o valor crítico da distribuição normal padrão (Z) tal que a probabilidade P(|Z| ≤ 1,96) = 95%. Então, o fabricante, ao nível de significância de 5%,