Seja 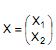um vetor de variáveis aleatórias e seja 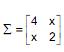sua matriz de covariâncias. Seja λ a primeira componente principal da matriz ∑ . Sabendo que a proporção da variância total de X que é explicada por λ é 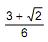o valor de x é

Uma variável aleatória U tem distribuição uniforme contínua no intervalo [α, 3α]. Sabe-se que U tem média 12. Uma amostra aleatória simples de tamanho n, com reposição, é selecionada da distribuição de U e sabe-se que a variância da média dessa amostra é 0,1. Nessas condições, o valor de n é

Uma amostra aleatória simples de tamanho n é tomada de uma população de tamanho N. Sabe-se que N = 10 n e que a variância populacional é σ². A variância da média amostral é dada por

Para o modelo ARIMA(0,0,2) dado por

X_t = θ₀ + a_t − θ₁ a_{t − 1} − θ₂ a_{t − 2}, onde a_t é o ruído branco de média zero e variância σ², e θ₀ é uma constante, considere as seguintes afirmações:

I. O processo resultante desse modelo é sempre estacionário.

II. O processo resultante desse modelo só é estacionário se estiverem satisfeitas simultaneamente as condições −1 < θ₂ < 1,
θ₂ − θ₁ < 1 e θ₂ + θ₁ < 1.

III. A função de autocorrelação parcial do processo resultante desse modelo é dominada por uma mistura de exponenciais ou senoides amortecidas.

IV. A função de autocorrelação do processo resultante desse modelo apresenta decaimento exponencial.

Dentre as afirmações acima são verdadeiras APENAS