Uma assistente social realizou um estudo sobre o perfil econômico de 40 famílias de determinado bairro, selecionadas aleatoriamente. O interesse principal dessa assistente era classificar o nível salarial de cada família em A ou B, em que A indica que a família possui uma renda superior a R$ 3.500 e B indica que a família possui uma renda inferior ou igual a R$ 3.500. Também, ela objetivava categorizar a quantidade de membros de cada família em C ou D, em que C indica que a família é composta de 6 ou mais pessoas e D indica que a família é composta de, no máximo,5 pessoas. Não havendo outros níveis nem outras categorias a serem analisadas, ao final desse estudo, verificou-se que:
• 20% das famílias foram classificadas em nível A;
• 50% das famílias que foram classificadas em nível A também foram categorizadas com D;
• 40% das famílias foram categorizadas em C.
Se essa assistente pretende sortear aleatoriamente uma das famílias selecionadas para esse estudo, a probabilidade de que ela sorteie uma família do nível B e da categoria C é igual a

Francisco é pai de dois filhos: João e Maurício. Francisco deixou uma questão de Probabilidade para que ambos tentassem resolvê-la. A probabilidade de que João resolva a questão corretamente é 1/6, e a de que Maurício resolva essa mesma questão corretamente é 1/5 . Se ambos tentarem resolver a questão de forma independente, qual é a probabilidade de que no máximo um deles a resolva corretamente?

Um dado, com seis faces numeradas de 1 a 6, é viciado, de tal forma que a probabilidade de sair uma determinada face é proporcional ao seu valor (por exemplo, a face 6 é três vezes mais provável de sair do que a face 2). Ao lançar o dado e observar a face voltada para cima, qual é a probabilidade de ter sido obtido o número 6, sabendo-se que a face obtida é par?

Com relação ao cálculo de probabilidades podemos afirmar, exceto:

Com relação a função definida por mais de uma sentença a seguir,

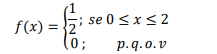
Podemos afirmar que: