Questões de Concurso
Filtrar
189 Questões de concurso encontradas
Página 9 de 38
Questões por página:
Questões por página:
Concurso:
Prefeitura Municipal de Rio Claro - S
Disciplina:
Física
Um corpo que desenvolve um movimento uniformemente variado tem o gráfico do espaço percorrido pela velocidade ao quadrado mostrada a seguir:
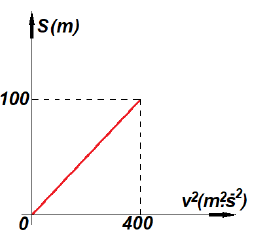
Após analisar o gráfico, conclui-se que a aceleração do corpo é
Concurso:
Prefeitura Municipal de Rio Claro - S
Disciplina:
Física
Um avião decola de Brasília no horário local às 19 ℎ 50 min e chega a Campo Grande – MS às 19 ℎ 45 min do mesmo dia no horário local. Se o trajeto feito pelo avião é de 880 min , a velocidade média no percurso foi de
Atente para a seguinte figura, que representa um cilindro, de raio R, que rola num plano horizontal na direção xi, sem deslizar.

No cilindro, existe um ponto P, localizado a uma distância R/3 do centro, inicialmente localizado acima do centro. Depois de três voltas completas do cilindro, o vetor deslocamento do ponto P é

No cilindro, existe um ponto P, localizado a uma distância R/3 do centro, inicialmente localizado acima do centro. Depois de três voltas completas do cilindro, o vetor deslocamento do ponto P é
Considere uma massa puntiforme que, saindo do repouso, se desloca de modo que a componente x de seu vetor aceleração é dada por ax=3t3, onde t é o tempo. A componente x da velocidade dessa partícula é descrita por
Uma partícula que executa um movimento harmônico simples ao longo do eixo x tem sua dinâmica descrita por uma equação do tipo a seguir, com a constante ⍵ positiva: