Questões de Concurso
Filtrar
37 Questões de concurso encontradas
Página 3 de 8
Questões por página:
Questões por página:
Disciplina:
Matemática
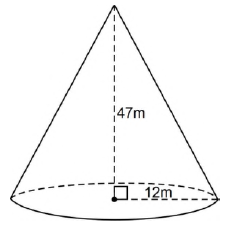
Assinale a alternativa que apresenta o volume do cone abaixo.
π = 3,14
Concurso:
Prefeitura de Lucas do Rio Verde - MT
Disciplina:
Matemática
O interior de uma taça usada para drinks tem a forma de um cone circular reto com diâmetro 1,2 dm e altura 8 cm.
Usando π=3, o volume máximo de líquido, em cm³, que cabe nessa taça é:
Usando π=3, o volume máximo de líquido, em cm³, que cabe nessa taça é:
Concurso:
Prefeitura de Sapezal - MT
Disciplina:
Matemática
Em um cone reto, o raio da base, a altura e a geratriz, nessa ordem, formam uma progressão aritmética. Logo, a planificação da superfície lateral desse cone é um setor circular, cujo ângulo central, em radianos, é igual a:
Disciplina:
Matemática
mostrar texto associado
ALERT: Essa questão ainda está sendo revisada pela equipe FonteConcursos!
Disciplina:
Matemática
mostrar texto associado
Visualizar Questão Comentada
Com base nessa situação hipotética, julgue o item que se segue.
O plano perpendicular ao segmento AB que contém o ponto A determina um círculo máximo na esfera e uma parábola no cone.
