Questões de Concurso
Filtrar
96 Questões de concurso encontradas
Página 5 de 20
Questões por página:
Questões por página:
Disciplina:
Física
Do trabalho “Galileu contra a inércia circular” de Júlio C. R. de Vasconcelos é retirado o seguinte trecho:
“[...] deve-se observar que um grau de velocidade qualquer, uma vez comunicado a um móvel, imprime-se nele de forma indelével por sua própria natureza, desde que não intervenham causas externas de aceleração ou retardamento; [...] (EN,8, p.243; Galileu Galilei, Duas novas ciências; Trad. de L. Mariconda & P. R. Mariconda. São Paulo: Nova Stella,1988., p.213). (...) A título de conclusão, propõe-se que este é o enunciado que melhor caracteriza a ______ de Galileu; (...) sua decidida e firme escolha é pela afirmação da preservação do grau de velocidade, seja qual for o movimento que estiver sendo considerado.”
Fonte: Vasconcelos (Scientiae Studia v.3, n.3, p.395,2005).
Assinale, entre as alternativas abaixo, aquela que corretamente preencha a lacuna da citação e apresenta um parágrafo compatível com as obras galileana e newtoniana.
“[...] deve-se observar que um grau de velocidade qualquer, uma vez comunicado a um móvel, imprime-se nele de forma indelével por sua própria natureza, desde que não intervenham causas externas de aceleração ou retardamento; [...] (EN,8, p.243; Galileu Galilei, Duas novas ciências; Trad. de L. Mariconda & P. R. Mariconda. São Paulo: Nova Stella,1988., p.213). (...) A título de conclusão, propõe-se que este é o enunciado que melhor caracteriza a ______ de Galileu; (...) sua decidida e firme escolha é pela afirmação da preservação do grau de velocidade, seja qual for o movimento que estiver sendo considerado.”
Fonte: Vasconcelos (Scientiae Studia v.3, n.3, p.395,2005).
Assinale, entre as alternativas abaixo, aquela que corretamente preencha a lacuna da citação e apresenta um parágrafo compatível com as obras galileana e newtoniana.
Disciplina:
Física
Em 1638 Galileu Galilei publicou o livro Discurso sobre as Duas Novas Ciências (Discorsi e dimostrazioni matematiche, intorno a due nuove scienze) que reúne quantidade significativa de seu trabalho nos anos anteriores. Considere as afirmativas a seguir.
I. Neste livro é apresentado o famoso experimento do plano inclinado. II. Galileu foi condenado à prisão domiciliar (perpétua) pelo tribunal da inquisição por conta desta publicação. III. As duas novas ciências são: a cinemática e o que modernamente se tornou a ciência de materiais. IV. As duas novas ciências são: a ciência aristotélica e a física clássica.
Estão corretas as afirmativas:
I. Neste livro é apresentado o famoso experimento do plano inclinado. II. Galileu foi condenado à prisão domiciliar (perpétua) pelo tribunal da inquisição por conta desta publicação. III. As duas novas ciências são: a cinemática e o que modernamente se tornou a ciência de materiais. IV. As duas novas ciências são: a ciência aristotélica e a física clássica.
Estão corretas as afirmativas:
Disciplina:
Física
Observe o experimento a seguir.
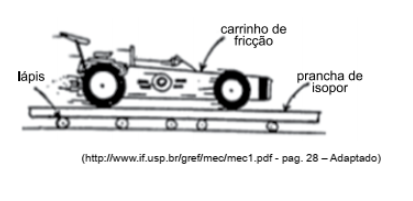
Considere que a massa do carrinho é maior do que a massa da prancha de isopor. Ao colocar o carrinho com as rodas friccionadas em cima da prancha, o vetor resultante do movimento da prancha será
Concurso:
Prefeitura Municipal de Rio Claro - S
Disciplina:
Física
18 - Ao se aplicar três forças ( 
= 30 N, 
= 40 N e 
= 50 N) em um ponto, observa-se que a força resultante
= 30 N, = 40 N e = 50 N) em um ponto, observa-se que a força resultante Uma força F atua em uma massa puntiforme m, que tem seu vetor posição descrito por R=1∙sen(2πt+π)j, onde j é o vetor unitário na direção y. Assim, essa força é dada por
