Questões de Concurso
Filtrar
304 Questões de concurso encontradas
Página 3 de 61
Questões por página:
Questões por página:
A física é fundamentalmente uma ciência experimental. O aprendizado metodológico da aplicação de matemática a fenômenos naturais têm grande valor no desenvolvimento intelectual de jovens e adultos ao tornar objetiva a exploração desta tradição do pensamento humano de submeter a realidade à modelagem matemática e sua verificação experimental em caráter estatístico. Em um site de educação encontra-se por exemplo essa proposta de atividade utilizando um pêndulo simples: “Um dos possíveis experimentos de baixo custo que podem ser desenvolvidos em sala de aula envolve o pêndulo simples. Com ele, é possível medir o valor da aceleração da gravidade local sem muitas complicações.”.
Fonte:https://educador.brasilescola.uol.com.br/estrategias-ensino/medindo-gravidade-com-um-pendulo-simples-sala-aula.htm
Considerando que entre os diferentes comprimentos de fio que o professor usará para demonstrar que o modelo é adequado, um deles será 40 cm. A massa de prova é suficientemente grande para que os efeitos do arrasto com o ar sejam desprezíveis no movimento do pêndulo (viabilizando a aplicação do modelo do pêndulo simples). Um grupo de 10 estudantes cronometram o movimento de 10 oscilações do pêndulo com seus celulares, enquanto o restante da sala animadamente conta as oscilações.
O professor, antes de executar o experimento, na preparação da aula, chegou aos valores de comprimento, de modo que fossem compatíveis para as medições que serão obtidas nos cronômetros dos estudantes. Ele usou g = 10 m/s2 e pi = 3. Assinale a alternativa que identifica corretamente a estimativa produzida para o pêndulo de 40 cm de comprimento.
Fonte:https://educador.brasilescola.uol.com.br/estrategias-ensino/medindo-gravidade-com-um-pendulo-simples-sala-aula.htm
Considerando que entre os diferentes comprimentos de fio que o professor usará para demonstrar que o modelo é adequado, um deles será 40 cm. A massa de prova é suficientemente grande para que os efeitos do arrasto com o ar sejam desprezíveis no movimento do pêndulo (viabilizando a aplicação do modelo do pêndulo simples). Um grupo de 10 estudantes cronometram o movimento de 10 oscilações do pêndulo com seus celulares, enquanto o restante da sala animadamente conta as oscilações.
O professor, antes de executar o experimento, na preparação da aula, chegou aos valores de comprimento, de modo que fossem compatíveis para as medições que serão obtidas nos cronômetros dos estudantes. Ele usou g = 10 m/s2 e pi = 3. Assinale a alternativa que identifica corretamente a estimativa produzida para o pêndulo de 40 cm de comprimento.
Disciplina:
Física
O sistema mostrado na figura a seguir é uma máquina de Atwood que consiste numa polia de massa 2kg e raio R, que pode girar em torno do eixo fixo passando pelo centro da polia. Os dois blocos, de massa 2kg e 1kg, estão ligados por um fio inextensível de massa desprezível. 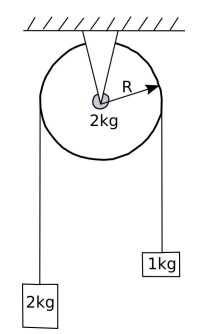
Desprezando todos os atritos e sabendo que os blocos são abandonados do repouso, pode-se concluir que o módulo da aceleração dos blocos é:

Desprezando todos os atritos e sabendo que os blocos são abandonados do repouso, pode-se concluir que o módulo da aceleração dos blocos é:
Disciplina:
Física
Um sistema formado por duas massas idênticas, unidas por uma barra rígida de massa desprezível e comprimento b, repousa sobre um plano horizontal sem atrito. Uma partícula de massa m desloca-se sem influências de atritos e velocidade V0 sobre o plano horizontal, perpendicularmente ao sistema de duas massas, e colide frontalmente com a massa m inferior, ficando colada a ela (fig).
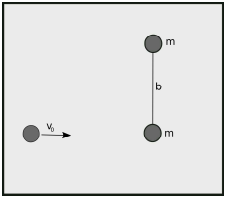
Após a colisão, a velocidade angular do sistema em torno do centro de massa é:

Após a colisão, a velocidade angular do sistema em torno do centro de massa é:
Disciplina:
Física
Duas partículas de massas m1 = m e m2 = 2m formam um sistema isolado. Seja 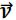 a velocidade da partícula de massa m2 em relação a m1 e
a velocidade da partícula de massa m2 em relação a m1 e 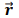 o vetor de posição de m2 em relação a m1. O momento angular total do sistema relativo ao centro de massa é:
o vetor de posição de m2 em relação a m1. O momento angular total do sistema relativo ao centro de massa é:
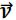 a velocidade da partícula de massa m2 em relação a m1 e
a velocidade da partícula de massa m2 em relação a m1 e 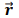 o vetor de posição de m2 em relação a m1. O momento angular total do sistema relativo ao centro de massa é:
o vetor de posição de m2 em relação a m1. O momento angular total do sistema relativo ao centro de massa é:
Disciplina:
Física
Suponha que um trem esteja se movimentando numa curva de raio de curvatura R a uma velocidade de valor constante v. Se a distância entre os trilhos é D e a intensidade da gravidade é g, a altura que é preciso levantar o trilho externo para minimizar a pressão que o trem exerce sobre ele, ao passar pela curva, é: