Questões de Concurso

A “Lei de resfriamento de Newton” consiste de um modelo simples para a dinâmica da temperatura T de um corpo inicialmente a uma temperatura T₀ , que troca calor com o ambiente, a uma temperatura TR < T₀, em uma taxa proporcional apenas à diferença entre a temperatura do corpo e do meio exterior. A taxa de condução do calor entre o corpo e o meio que depende de características físicas como a superfície de contato entre o corpo e o meio é contabilizada em termos efetivos pela constante positiva k. A equação do modelo está representada na imagem abaixo. No gráfico temos o resultado do experimento conduzido para uma pequena quantidade de glicerina (10 cm³ ) em um tubo de ensaio a uma temperatura inicial T₀ =100ºC sendo a temperatura do ambiente TR = 21ºC. O perfil observado é aproximadamente exponencial. Considerando 1/e = 0,37. O valor da constante k para esse experimento é de aproximadamente:

No diagrama abaixo temos o desenho em escala de um automóvel. As linhas cinzas indicam a posição das molas dianteiras e traseiras bem como do centro de massa do automóvel (posicionado na intersecção entre as duas faixas cinzas correspondentes). Em virtude do motor ser um dos componentes de maior massa em carros de tração dianteira o centro de massa em geral fica mais próximo da frente (onde ele é disposto) do que da traseira. Admita que as molas tanto traseiras quanto dianteiras tenham mesmo comprimento e que o carro é regulado para estar no nível (prumo) com a mesma compressão sobre todas elas. Sobre as constantes elástica das molas dianteiras, k_D, e traseiras, k_T, assinale a alternativa correta.

Assinale a alternativa correta. Realiza-se um experimento didático de choque unidimensional entre dois corpos de massas M e m, onde M = 2m, que flutuam sobre um trilho de ar (atritos são considerados desprezíveis). Os corpos são inicialmente impulsionados um contra o outro por molas de constante elástica k a partir de uma mesma deformação x das molas (novamente desconsiderando-se forças dissipativas). A distância entre os corpos é muito maior que os comprimentos de elongação das molas. Ao se encontrarem o uso de uma massa aderente sobre um deles permite que o choque seja perfeitamente inelástico. As velocidades antes e após o choque pode ser avaliada por um sistema de foto de longa exposição e um estroboscópio. A velocidade do conjunto dependerá da velocidade inicial e, portanto, de k e de x, com respeito ao valor da massa m a velocidade do conjunto após o choque:

A velocidade mínima com que se deve lançar um corpo da superfície de um planeta (foguete, míssil ou um satélite) para que ele vá para o infinito, nunca mais retornando, é denominada de velocidade de escape. A velocidade de escape (v_e) é obtida a partir da condição de que, no infinito, a energia mecânica do corpo lançado é nula. Logo, V_e = √ 2GM/R, onde: R é o raio equatorial do planeta; G é uma constante de proporcionalidade gravitacional; e M é a massa do planeta. Por exemplo, para a Terra, a velocidade de escape é de, aproximadamente,11,2 km/s.
Internet: <www.if.ufrgs.br> (com adaptações).
Considere-se um foguete lançado com uma velocidade v_s. Para escapar do planeta, o foguete precisará atingir uma velocidade de escape (v_e) correspondente a

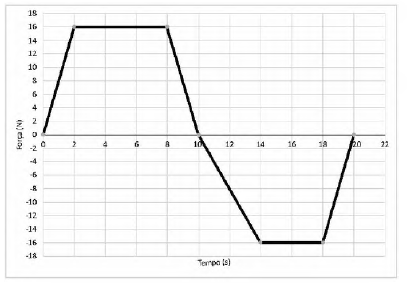
Um corpo de 10 kg move-se ao longo do eixo x sob a ação de uma força que o impulsiona. A figura abaixo mostra a força que age sobre o corpo, que parte do repouso, em t = 0.

Com base nesse caso hipotético, o valor do módulo da velocidade do corpo, em metros por segundo, no instante t = 20 s é igual a