Filtrar
8 Questões de concurso encontradas
Página 1 de 2
Questões por página:
O método dos Mínimos Quadrados Ordinários (MQO) apresenta propriedades estatísticas que o tornam um dos métodos mais populares e eficientes de análise de regressão.
A eficiência desse método depende da validade da seguinte hipótese:
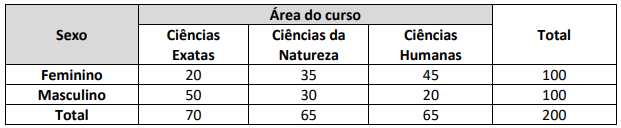
Nesse contexto, denote: • X = número esperado, sob a suposição de independência, de estudantes do sexo Feminino que escolheram um curso na área de Ciências Exatas;
• Y = graus de liberdade da estatística do teste qui-quadrado associado.
Com base nos dados fornecidos, os valores de X e Y são, respectivamente:
No teste da hipótese de que a variância de uma população é igual ao valor fixo σ02 ,
ou seja, H0 : σ2 = σ02, usa-se a estatística
em que s2 é a estimativa da variância calculada com base em uma amostra composta por n observações. Essa estatística possui uma distribuição qui-quadrado com certo número de graus de liberdade. Foi aplicado um teste para a hipótese citada em uma amostra com 15 observações. Então, é correto afirmar que a esperança matemática (média) e a variância de uma variável aleatória com a distribuição descrita são, respectivamente,
Para testar a variância de uma medida, um estatístico resolve usar a distribuição Qui-Quadrado, dadas as probabilidades:
As hipóteses são as seguintes:
Ho: σ2 = 15 contra Ha: σ2 ≠ 15
A partir de uma amostra com 11 observações, conclui-se que:
