Questões de Concurso
Filtrar
298 Questões de concurso encontradas
Página 11 de 60
Questões por página:
Questões por página:
Concurso:
Prefeitura de Aracaju - SE
Disciplina:
Matemática
mostrar texto associado
Visualizar Questão Comentada
De acordo com essas informações, julgue o item seguinte.
A expressão y2 + x2 = 1 não pode ser usada para definir uma função.
Concurso:
Prefeitura de Ivaí - PR
Disciplina:
Matemática
A respeito da representação gráfica da função linear f(x) = - 2x / 5 + 8, é correto dizer que:
Concurso:
Prefeitura de Guaíra - PR
Disciplina:
Matemática
Uma função do primeiro grau é dada por f(x) = 2x - 5. Qual o valor de f(3)?
Concurso:
Banco da Amazônia
Disciplina:
Matemática
A Figura apresenta uma região do plano cartesiano, destacada na cor cinza, que é limitada por uma reta e por uma parábola.
A região em destaque é constituída pelos pontos (x, y) cujas coordenadas satisfazem o seguinte sistema de inequações:
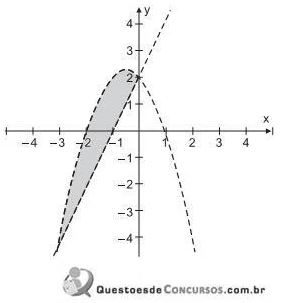
A região em destaque é constituída pelos pontos (x, y) cujas coordenadas satisfazem o seguinte sistema de inequações:
Considere as funções reais f e g, definidas a seguir para todo 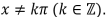
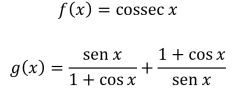
Considere agora a função h definida por h(x) = f(x) + g(x). O menor valor positivo pertencente ao conjunto imagem de h é igual a: