2. Questões de Concurso
  3. Matemática
  4. Assunto - Função Logarítmica

Filtrar

Questões por página:
Se 3log3 x + 9log9 x = 2, então o valor de x é:
Se log 5 = 0,70 e log 7 = 0,85, então qual é o valor de log 35?
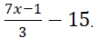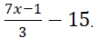Dada a função g tal que g(x) = Imagem associada para resolução da questão Qual é o valor de g (7)?
Em um estudo sobre o crescimento populacional de uma espécie de peixes em um lago, foi utilizado um modelo matemático baseado em uma função logarítmica para descrever o aumento da população ao longo do tempo. A função utilizada é P(t) = k ∗ log(t + 1), onde P(t) representa o número de peixes no lago após t semanas, k é uma constante que reflete a taxa de crescimento populacional, e t é o tempo, em semanas, desde o início da observação. Durante a pesquisa, constatou-se que após 7 semanas, o lago abrigava 896 peixes. Com base nesses dados, determine o valor da constante k que regula o crescimento populacional da espécie e calcule o número aproximado de peixes no lago ao final de 15 semanas.
Um grupo de cientistas está estudando o crescimento populacional de uma determinada espécie de inseto em uma região específica. Eles observaram que o crescimento populacional dos insetos segue um padrão logarítmico, e desejam modelar essa situação para prever a população futura e planejar estratégias de controle, se necessário.
Os cientistas coletaram dados ao longo de vários anos e descobriram que o número de insetos, N, em uma determinada época t, pode ser representada pela função logarítmica N(t) = 200000 ∙ log(t + 52)+ 500000, onde t representa o tempo em meses.
Considerando a função logarítmica apresentada, o número de insetos na população, quando t = 4 anos, será de
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo