2. Questões de Concurso
  3. Estatística
  4. Assunto - Funções de Probabilidade p(x) e Densidade f(x)

Filtrar

Questões por página:
Sua consulta médica está marcada para 15h. Você pode tomar um dentre dois caminhos para chegar ao consultório. Pelo primeiro caminho, você demora em média 30 minutos, com desvio padrão de 10 minutos, para chegar ao consultório, segundo uma distribuição normal. Pelo segundo caminho, o tempo médio do trajeto até o consultório é de 25 minutos, com desvio padrão de 5 minutos, também segundo uma distribuição normal. São 14:35. O caminho que tem maior probabilidade de te levar ao consultório no horário marcado é:
Em relação à geração de números aleatórios por computadores, analise as afirmativas abaixo.
I. Chama-se semente o número que inicia o algoritmo de geração de números pseudoaleatórios.
II. Os números comumente gerados por um computador como aleatórios são, na verdade, pseudoaleatórios, uma vez que há um algoritmo que gera esses números.
III. Caso o algoritmo gere em algum momento o número usado como semente, a sequência de números pseudoaleatórios deverá se repetir.
IV. Os computadores têm, internamente, um gerador de números verdadeiramente aleatórios.
Estão corretas as afirmativas:
Se chover hoje à noite, Maria não vai sair. Se não sair, a probabilidade de pedir uma pizza para entrega em casa é de 0,80. Por outro lado, se não chover Maria vai sair, e, nesse caso, a probabilidade de ir a uma pizzaria e pedir uma pizza para consumo no local é de 0,20. Sabendo que a probabilidade de chover hoje à noite é de 0,25, a probabilidade de Maria pedir uma pizza é de:

A função densidade de probabilidade f(t) = 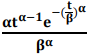Imagem associada para resolução da questão t > 0, e α, β > 0 corresponde ao tempo até falhar de um equipamento eletrônico e corresponde à distribuição Weibull com parâmetros α e β. Essa distribuição é usada no dimensionamento do tempo de garantia de um produto eletrônico a ser adquirido por uma instituição judiciária. Então, a diretoria da instituição quer saber da equipe técnica a probabilidade de o equipamento falhar dentro do prazo de 1 ano. A equipe técnica pesquisa o banco de dados da rede de assistência técnica do fabricante do equipamento e, com os dados registrados do tempo de falha do produto, estima os parâmetros α e β em 2 e 5. Dessa forma, é correto afirmar que a probabilidade de falha dentro do prazo de 1 ano é

Considere que o tamanho de certa população é muito maior que o da amostra e que a probabilidade de z ser menor ou igual a 2 é de aproximadamente 0,975 (P( z ≤2)~0,975).
Com base nisso, o tamanho mínimo da amostra para estimar uma proporção P, com base em uma amostra aleatória simples, com margem de erro de 5% e probabilidade de 95%, é:
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo