Filtrar
194 Questões de concurso encontradas
Página 1 de 39
Questões por página:
Questões por página:
Concurso:
Polícia Científica - PR
Disciplina:
Matemática
Um rapaz atirou um disco de uma certa massa, e o mesmo descreveu uma parábola com a função dada por 60x – x2. Com base nestes dados, e sabendo que a unidade do sistema é em centímetros, a altura máxima em metros alcançada pelo disco foi de:.
Mário começou a praticar um novo jogo que adquiriu para seu vídeo-game. Considere que a cada partida ele conseguiu melhorar sua pontuação, equivalendo sempre a 15 pontos a menos que o dobro marcado na partida anterior. Se na quinta partida ele marcou 3.791 pontos, então, a soma dos algarismos da quantidade de pontos adquiridos na primeira partida foi igual a
Concurso:
Prefeitura de Santa Leopoldina - ES
Disciplina:
Matemática
A figura abaixo é de um cone que tem o volume V= 37,68 cm³ e cujo raio da base é r = 3 cm. Fazendo π= 3,14, a medida de g é: 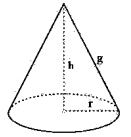

Concurso:
Prefeitura de Macaé - RJ
Disciplina:
Matemática
Sejam A, B, C e D pontos distintos sobre uma reta r. O ponto B está entre A e D e o ponto D entre B e C.
É correto afirmar que
Concurso:
Prefeitura de Caraguatatuba - SP
Disciplina:
Matemática
Em um plano cartesiano, os vértices de um quadrilátero convexo são representados pelos pontos A(1,1), B(5,4), C(5,9) e D(1,6). Com base nessas informações, é possível concluir que o tal quadrilátero é um