Questões de Concurso

A figura seguinte, cujas dimensões estão indicadas em metros, mostra as regiões R1 e R2, ambas com formato de triângulos retângulos, situadas em uma praça e destinadas a atividades de recreação infantil para faixas etárias distintas.

Se a área de R1 é 54 m², então o perímetro de R2 é, em metros, igual a

A figura representa um terreno retangular dividido por um muro CFOP, sendo CF e OP paralelos ao lado menor, FO paralelo ao lado maior do terreno, medindo, respectivamente, 24m, 6m e 25m. Para a finalidade a que se destina, foi constatado que as duas partes em que o terreno está dividido seriam mais bem aproveitadas se, sem alterar a medida de suas áreas, o muro existente fosse substituído por outro, em linha reta. Por questões técnicas, como o novo muro não pode ser paralelo aos lados do terreno, optou-se por um muro obliquo, como indicado pelo segmento CM.
Nessas condições, pode-se afirmar que CM divide FO em dois segmentos FR e RO, tais que a razão entre suas medidas é um valor pertencente ao intervalo

Na figura, os segmentos CB e DM representam duas escadas cujas extremidades superiores C e D apoiam-se em uma parede vertical e as extremidades inferiores, B e M, apoiam-se, respectivamente no solo e em CB.
Sabendo-se que as duas escadas têm a mesma medida de comprimento — 1,20m — pode-se afirmar que a medida de H, em metros, é igual a

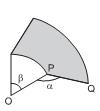
Com relação à figura apresentada,

• o segmento OP representa a haste à qual é fixada a lâmina de borracha PQ, do limpador de parabrisa do vidro traseiro de um automóvel, segundo um ângulo constante α = 150^o ;
• a região sombreada representa a área A, varrida por PQ quando OP faz uma rotação em torno do centro O, de um ângulo ß, no sentido anti-horário;

Sendo pode-se afirmar que uma expressão válida para A, em u.a., é

Quatro amigos resolveram repartir uma pizza circular, em porções, na forma de setores, diretamente proporcionais ás suas respectivas idades.

Se essas idades somam 72 anos e seus numerais formam uma progressão aritmética de razão r = 4, então a tangente trigonométrica do menor dos ângulos θ1, θ2, θ3, θ4 é igual a