Filtrar
31 Questões de concurso encontradas
Página 1 de 7
Questões por página:
Questões por página:
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Calcule a integral por partes da função:
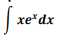
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Considere a função f (x) = 3x2 - 4x +1. Calcule a integral definida de f (x) no intervalo [1,3].
Disciplina:
Matemática
Considerando que 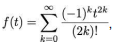 a alternativa correta que contém, respectivamente,
a alternativa correta que contém, respectivamente, 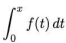 e raio de convergência de f(t) é:
e raio de convergência de f(t) é:
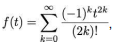 a alternativa correta que contém, respectivamente,
a alternativa correta que contém, respectivamente, 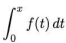 e raio de convergência de f(t) é:
e raio de convergência de f(t) é:
Disciplina:
Matemática
Uma solução para a integral indefinida 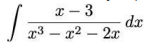 está na alternativa:
está na alternativa:
Disciplina:
Matemática
Calculando o valor da integral definida, a seguir,  obtemos o resultado que está na alternativa:
obtemos o resultado que está na alternativa:
 obtemos o resultado que está na alternativa:
obtemos o resultado que está na alternativa: