Filtrar
29 Questões de concurso encontradas
Página 1 de 6
Questões por página:
Questões por página:
Concurso:
EBSERH
Disciplina:
Estatística
Questão Anulada
Um fabricante de cerveja pretende construir um intervalo de 90% de confiança para o conteúdo médio das latas. Se o desvio padrão do conteúdo é de 15 ml e o erro não deve ultrapassar 2 ml, assinale a alternativa que apresenta o tamanho de amostra que o fabricante deve utilizar.
A Tabela 1 deve ser utilizada na solução da questão.
Tabela da distribuição normal padronizada – P(0≤Z≤z)
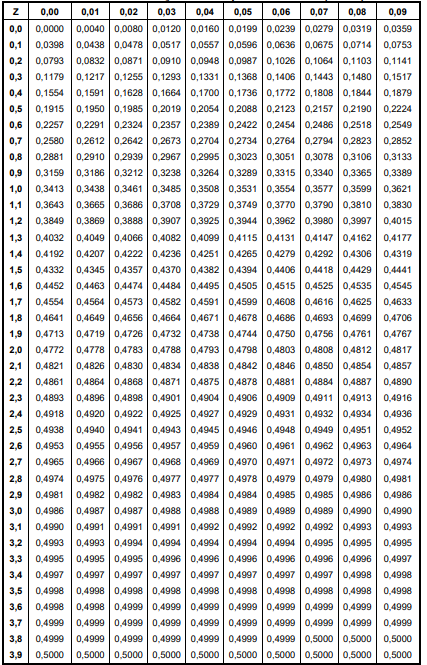
Tabela 1 Fonte: Stevenson, W.J.1986. Estatística aplicada à administração. São Paulo, Harbra, p.461
A Tabela 1 deve ser utilizada na solução da questão.
Tabela da distribuição normal padronizada – P(0≤Z≤z)
Tabela 1 Fonte: Stevenson, W.J.1986. Estatística aplicada à administração. São Paulo, Harbra, p.461
Concurso:
TRF - 2ª REGIÃO
Disciplina:
Estatística
Se a variável aleatória X tem distribuição normal com média μ e variância σ2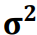
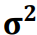, ou seja, X ⁓ N(μ, σ2), s2 = 
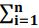(xi–x̄)2/n–1 (variância amostral) é a estimativa de σ2 com base em uma amostra com n observações, [x1, x2, ..., xn]. Assim, a variável T = X – μ/s tem distribuição t de Student com n – 1 graus de liberdade, ou seja, T ~ tn-1. Nesse caso, sabendo que P(T ≤ 2) = 0,968027 e P(T ≥ -2) = 0,031973, é correto afirmar que
Concurso:
Receita Federal
Disciplina:
Estatística
Uma amostra aleatória de tamanho n = 64 de uma variávelaleatória suposta normalmente distribuída com médiadesconhecida μ e variância 100 foi observada e revelou uma médiaamostral igual a 44,65.
Lembrando que se Z tem distribuição normal padrão,
P[- 1,96 < Z < 1,96] = 0,95,
o intervalo de 95% de confiança para μ será dado por
Lembrando que se Z tem distribuição normal padrão,
P[- 1,96 < Z < 1,96] = 0,95,
o intervalo de 95% de confiança para μ será dado por
De uma amostra aleatória de tamanho 64 extraída, com reposição, de uma população normalmente distribuída e variância conhecida σ2, obteve-se um intervalo de confiança de 95% igual a [23,27] para a média μ desta população. Desejando-se obter um intervalo de confiança de 95% para μ, porém com amplitude igual à metade da obtida anteriormente, é necessário extrair da população uma amostra aleatória, com reposição, de tamanho
Num processo produtivo foi selecionada uma amostra de 270 peças, selecionadas ao final de sua linha de produção; destas,10% estavam com algum tipo de inconsistência com os padrões necessários de qualidade. Com 90% de confiança, determine os valores (limite inferior e limite superior) mais próximos do intervalo, referente à população da proporção das peças geradas neste processo produtivo que estão consistentes com os padrões necessários de qualidade.
