Filtrar
139 Questões de concurso encontradas
Página 1 de 28
Questões por página:
Questões por página:
Concurso:
CAU-MA
Disciplina:
Estatística
mostrar texto associado
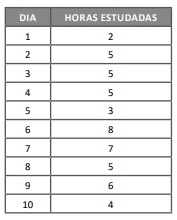
Com base nessa situação hipotética e nos dados apresentados, julgue o item a seguir.
A variância do número de horas estudadas por Gael nesses dez dias é igual a 3,2.
Concurso:
Prefeitura de Goiânia - GO
Disciplina:
Estatística
Em estatistíca, a variância é um numero que apresenta a unidade elevada ao quadrado em relaqao a variável que não esta elevada ao quadrado, o que pode ser um inconveniente para a interpretação do resultado. Por isso, é mais comumente utilizada na estatistica descritiva o desvio-padrao, que é definido como
mostrar texto associado
Visualizar Questão Comentada
Com base na situação hipotética precedente, julgue o item que se segue.
O desvio padrão dos valores da amostra é inferior a R$ 18 mil.
Concurso:
PF
Disciplina:
Estatística
Considerando que de uma população X que se distribui conforme uma distribuição normal com média M e variância V foi retirada uma amostra aleatória simples de tamanho n = 4, denotada como X1, X2, X3, X4, julgue o item a seguir, a respeito da soma S = X1 + X2 + X3 + X4.
O desvio padrão da razão S/√V é igual a 2.
O desvio padrão da razão S/√V é igual a 2.
Concurso:
PF
Disciplina:
Estatística
mostrar texto associado
A partir da situação hipotética e com base na figura precedente, que mostra o diagrama de caixa (boxplot), julgue o item a seguir.
A amplitude interquartil é igual a R$ 20 mil.
A amplitude interquartil é igual a R$ 20 mil.
