Questões de Concurso
Filtrar
113 Questões de concurso encontradas
Página 18 de 23
Questões por página:
Questões por página:
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
A tabela de índices abaixo foi montada considerando o preço de custo unitário médio anual de determinado equipamento, em reais, em um período de 10 anos (entre 2008 e 2017). Foram considerados como índices os preços relativos, em porcentagens, adotando o preço de custo unitário médio anual do equipamento em 2010 como básico.
Se o preço de custo unitário médio deste equipamento, em 2014, era de R$ 25,30, então o acréscimo desse preço de 2008 para 2017 foi, em R$, de
Se o preço de custo unitário médio deste equipamento, em 2014, era de R$ 25,30, então o acréscimo desse preço de 2008 para 2017 foi, em R$, de
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Em uma repartição pública, o sistema de atendimento ao público é composto por somente um atendente e considera-se que tanto as chegadas na fila quanto o atendimento das pessoas são marcovianos (modelo M/M/1) e com uma população de tamanho infinito. Se o atendente demora, em média,10 minutos para atender uma pessoa e, em média,4 pessoas chegam na fila por hora, o tempo médio, durante o qual a pessoa fica na fila, é, em minutos, igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Em uma determinada data, o gerente comercial de uma fábrica de um produto marca X, concorrente somente com o produto de outro fabricante marca Y, insatisfeito com a participação de seu produto no mercado, decide fazer uma promoção de seu produto. Verifica então que com a promoção, mensalmente,90% dos clientes que consumiam X continuaram a consumir X e 70% dos que consumiam Y passaram a consumir X. Seja a matriz de transição T abaixo:
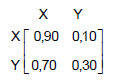
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
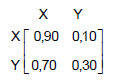
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Considere uma população P1 formada pela renda, em unidades monetárias (u.m.), dos 100 indivíduos que são sócios de um clube. Seja xi a renda, xi > 0, do sócio i.
Dados:
= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%.
Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Dados:
= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%. Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Uma população P de tamanho infinito tem distribuição normal com média μ e variância 2,25. A fim de proceder ao teste H₀: μ = 10 (hipótese nula) contra H₁: μ ≠ 10 (hipótese alternativa), ao nível de significância de 5%, extrai-se de P uma amostra aleatória de tamanho 100, estabelecendo-se a seguinte regra: “dado que 
é a média da amostra, então rejeita-se H₀ se 
< 10 − K ou 
> 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
é a média da amostra, então rejeita-se H₀ se < 10 − K ou > 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é 