Questões de Concurso
Filtrar
146 Questões de concurso encontradas
Página 25 de 30
Questões por página:
Questões por página:
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Em uma determinada data, o gerente comercial de uma fábrica de um produto marca X, concorrente somente com o produto de outro fabricante marca Y, insatisfeito com a participação de seu produto no mercado, decide fazer uma promoção de seu produto. Verifica então que com a promoção, mensalmente,90% dos clientes que consumiam X continuaram a consumir X e 70% dos que consumiam Y passaram a consumir X. Seja a matriz de transição T abaixo:
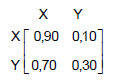
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
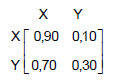
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Considere uma população P1 formada pela renda, em unidades monetárias (u.m.), dos 100 indivíduos que são sócios de um clube. Seja xi a renda, xi > 0, do sócio i.
Dados:
= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%.
Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Dados:
= 2.662.400 (u. m)2 e Coeficiente de variação de P1 igual a 20%. Decide-se excluir de P1 um total de 20 sócios que possuem renda igual à média de P1, formando uma nova população P2 com tamanho 80. O módulo da diferença, em (u.m.)2, entre as variâncias de P1 e P2 é de
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Uma população P de tamanho infinito tem distribuição normal com média μ e variância 2,25. A fim de proceder ao teste H₀: μ = 10 (hipótese nula) contra H₁: μ ≠ 10 (hipótese alternativa), ao nível de significância de 5%, extrai-se de P uma amostra aleatória de tamanho 100, estabelecendo-se a seguinte regra: “dado que 
é a média da amostra, então rejeita-se H₀ se 
< 10 − K ou 
> 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
é a média da amostra, então rejeita-se H₀ se < 10 − K ou > 10 + K, em que K > 0”. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 1,64) = 0,10, obtém-se que o valor de K é
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Uma amostra aleatória de tamanho 64 é extraída de uma população de tamanho infinito, normalmente distribuída, média μ e variância conhecida σ². Obtiveram-se com base nos dados desta amostra, além de uma determinada média amostral x,2 intervalos de confiança para μ aos níveis de 95% e 99%, sendo os limites superiores destes intervalos iguais a 20,98 e 21,29, respectivamente. Considerando que na curva normal padrão (Z) as probabilidades P(|Z| > 1,96) = 0,05 e P(|Z| > 2,58) = 0,01, encontra-se que σ² é igual a
Concurso:
TRT - 11ª Região (AM e RR)
Disciplina:
Estatística
Sejam X₁ e X₂ duas variáveis aleatórias independentes, ambas com média μ e variância 25. Como μ é desconhecida construiuse um estimador T para μ, sendo m e n parâmetros reais, ou seja: T = (m − 1)X₁ − nX₂. Considerando que T caracteriza uma classe de estimadores não viesados de μ, então o estimador desta classe mais eficiente verifica-se quando m for igual a
