Questões de Concurso

A forma geral de representar uma classe de séries temporais não estacionárias é o modelo utorregressivo integrado médias móveis de ordem (p, d, q), ou seja, ARIMA(p, d, q), em que p é o grau do polinômio aracterístico da parte autorregressiva Φ(B), q é o grau do polinômio característico da parte média móveis θ(B) e d é o grau de diferenciação ▽^d, ou seja, Φ(B)▽^dZ_t = θ(B)a_t em que ⊽^dZ_t = ω_t. Desse modo, tem-se Φ(B)ω_t = θ(B)a_t que é um modelo ARMA(p, q).

A uma determinada série temporal, ajustou-se um modelo da classe ARIMA(p, d, q), e os resultados do ajuste estão expostos a seguir:

Modelo ARIMA ajustado à série temporal

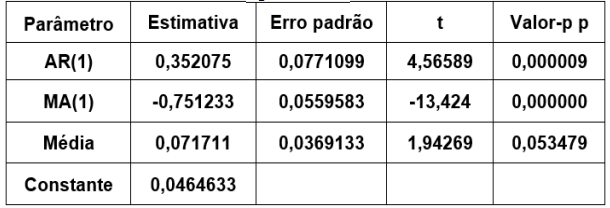
Então, é correto afirmar, com aproximação de três (03) casas decimais, que

Considere a seguinte série temporal:

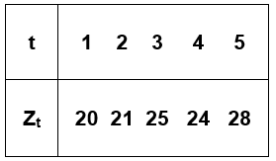
É correto afirmar que a média, a variância e a autocorrelação de defasagem 2 dessa série temporal, assumindo o estimador de máxima verossimilhança para a variância, são, respectivamente:

O estatístico que trata da análise de dados referentes à Justiça Federal necessita conduzir um estudo que requer informações sobre determinada característica quantitativa, X, dos processados em determinada Vara Federal. Um dos objetivos é construir um intervalo de 95% de confiança para o valor médio da característica quantitativa do grupo de processados, com erro de amostragem ou precisão de 0,5 σ, meio desvio-padrão. Ele tomou, então, uma amostra aleatória piloto de tamanho n₀ = 5 que forneceu as seguintes estatísticas amostrais, média e variância, para a característica: x̄₀ = 127,6 e S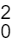 = 1290,8. A respeito das informações anteriores, sabe-se que é possível assumir o modelo de distribuição normal para a característica quantitativa do grupo de processados, que é finito com N = 2000 indivíduos e com variância desconhecida. Assim, conhecendo o escore da distribuição t de t₄ (0,975) = 2,78, é correto afirmar que o tamanho definitivo da amostra n é

Seja [X₁, X₂, ..., X_n] uma amostra aleatória de uma variável aleatória com distribuição normal, com média μ e variância σ², ou seja, X ⁓ N(μ, σ²), em que os parâmetros são desconhecidos, então, os estimadores uniformemente de mínima variância não viciados, UMVU, da média μ e variância σ² são, respectivamente,