Questões de Concurso
Filtrar
62 Questões de concurso encontradas
Página 8 de 13
Questões por página:
Questões por página:
Concurso:
Prefeitura de Ribeirão Preto - SP
Disciplina:
Matemática
Resolvendo-se uma equação quadrática no conjunto dos números complexos, observou-se que a soma das raízes dessa equação era igual a 4, e o produto dessas raízes era igual a 5. Logo, a diferença entre essas raízes é igual a
Concurso:
CBM-SE
Disciplina:
Matemática
O produto entre os números complexos z1 = 3 √2(cos45° + i.sen45°) e z2 = 2 + i, é igual a:
Questão Anulada
A soma dos números complexos z1 = z1 = √2(cos135° + i.sen135°) e z2 = 2 √2 (cos45° +i.sen 45° ) é:
Concurso:
CBM-DF
Disciplina:
Matemática
Dada a igualdade 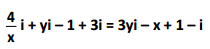 , a soma dos reais x e y é igual a:
, a soma dos reais x e y é igual a:
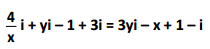 , a soma dos reais x e y é igual a:
, a soma dos reais x e y é igual a:
Questão Anulada
O conjunto solução da equação complexa |z – i| + |z + i| = 2 representa, no plano complexo, uma