2. Questões de Concurso

Filtrar

Questões por página:
No Microsoft Excel 2016, caso o usuário some o resultado das funções CONT.VALORES e CONTAR.VAZIO para um mesmo intervalo de células, ele terá como resultado:
Sobre a fórmula =A1&A2 do Microsoft Excel 2016, é correto afirmar que tem como resultado:
mostrar texto associado

Observe a planilha abaixo, criada no software Excel do pacote MSOffice 2016 BR.

 

Na planilha foi inserida uma expressão em E12 usando a função SE que mostra a mensagem “SUFICIENTE” se o conteúdo da célula C12 for igual ou menor que o da célula D12, e “ REPOR” caso contrário. Em seguida, a expressão inserida em E12 foi copiada para as células E13, E14, E15 e E16.

Nessas condições, uma expressão que poderia ser inserida na célula E15 está indicada na seguinte alternativa:

Sempre que uma planilha é criada, ela deve ser salva no disco rígido, com o objetivo de evitar que os dados sejam perdidos. Para isso, os softwares destinados a essa finalidade disponibilizam atalhos de teclado para execução. No Excel do pacote MSOffice 2013 BR e no Calc do pacote LibreOffice 5.1.0.3 esses atalhos de teclado são, respectivamente:

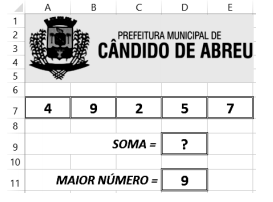
Observe a figura abaixo, que ilustra uma planilha criada no Excel 2010 BR.

Na célula D9 foi inserida a expressão =SOMA(A7;E7) Na célula D11 foi inserida uma expressão usando a função MAIOR que determina o maior número entre todos no intervalo de A7 a E7. Nessas condições, o número que deve aparecer em D9 e a expressão inserida em D11 são, respectivamente:
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo