Filtrar
505 Questões de concurso encontradas
Página 1 de 101
Questões por página:
Questões por página:
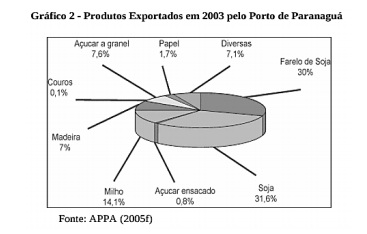
Considerando o gráfico apresentado na questão 09, qual a probabilidade de um lote, escolhido ao acaso, exportado em 2003 ter sido de milho ou soja?
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Matemática
Joana pretende enviar uma encomenda para Andreia por uma transportadora. A probabilidade de que Joana envie a encomenda é de 0,6. A probabilidade de que a transportadora não a perca ou a extravie é de 0,8. Por fim, a probabilidade de que o entregador a entregue é de 0,8. Dado que Andreia não recebeu a encomenda, qual é a probabilidade de que Joana não a tenha enviado?
Concurso:
Prefeitura de Araucária - PR
Disciplina:
Matemática
Um candidato fez prova de concurso em duas cidades diferentes. Em uma das cidades, a probabilidade de esse candidato passar na prova é de 30% e, na outra cidade, a probabilidade de ele passar é de 50%. Qual é a probabilidade de esse candidato passar em pelo menos uma dessas cidades?
Considere dois eventos A e B definidos em um mesmo espaço de probabilidades. Se P(A) = 0,4 e P(B) = 0,7, então é sempre correto afirmar que:
Três máquinas, A, B e C, produzem, respectivamente,35%,28% e 37% do número total de peças de uma fábrica. As porcentagens de peças defeituosas na produção dessas máquinas são, respectivamente,3%,2% e 5%. Uma peça é selecionada ao acaso e constata-se ser ela defeituosa. Encontre a probabilidade de a peça ter sido produzida pela máquina A. (Multiplique o resultado final por 100 e desconsidere as casas decimais).