Questões de Concurso
Filtrar
92 Questões de concurso encontradas
Página 4 de 19
Questões por página:
Questões por página:
Concurso:
Câmara de Marilândia - ES
Disciplina:
Matemática
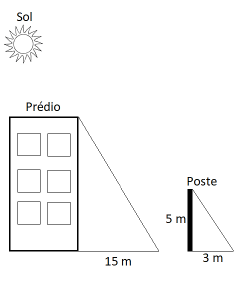
Analisando a figura a seguir, é possível observar que o Sol projeta uma sombra no prédio e no poste. Com base nisso e considerando a semelhança de triângulos, é correto afirmar que a altura do prédio, em metros, é igual a:

Concurso:
Prefeitura de Governador Lindenberg - ES
Disciplina:
Matemática
O marceneiro Carlos está fazendo uma mesa de canto que ficará em forma de um triângulo retângulo. As medidas das laterais devem ser 60cm e 80cm. A medida da frente desta mesa é:
Concurso:
Prefeitura de Fundão - ES
Disciplina:
Matemática
O Teorema de Pitágoras parece uma equação simples, mas tudo que é produzido por gênios como ele pode ser muito mais complexo do que parece. Neste caso existem variações que formam um grupo de equações chamado de "relações métricas no triângulo retângulo". Uma delas é a relação ( h² = m.n ). Usando estas informações encontraremos para m um valor de, aproximadamente: 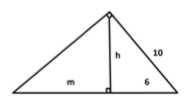

Concurso:
Prefeitura de Fundão - ES
Disciplina:
Matemática
O Teorema de Pitágoras parece uma equação simples, mas tudo que é produzido por gênios como ele pode ser muito mais complexo do que parece. Neste caso existem variações que formam um grupo de equações chamado de "relações métricas no triângulo retângulo". Uma delas é a relação ( h² = m.n ). Usando estas informações encontraremos para m um valor de, aproximadamente: 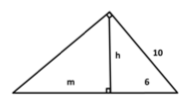

Concurso:
Prefeitura de São Roque do Canaã - ES
Disciplina:
Matemática
O Teorema de Pitágoras propõe uma relação entre os três lados de um triângulo retângulo, chamados de catetos e hipotenusa. Analise as afirmações abaixo e escolha a alternativa que corresponde à opção CORRETA.
I) A fórmula do Teorema de Pitágoras é a² = b² + c², onde a é a hipotenusa e b e c são os catetos. II) A fórmula do Teorema de Pitágoras é a² = b² + c², onde a é a hipotenusa e b e c são os catetos, mas pode ser alterada para b² = a² + c² ou c² = b² + a² sem modificar o resultado do cálculo. III) Se um triângulo retângulo tem catetos de medidas b = 7,5 cm e c = 10 cm, o valor da hipotenusa é a = 12,5 cm. IV) Se um triângulo retângulo tem catetos de medidas b = 7,5 cm e c = 10 cm, o valor da hipotenusa é a = 17,5 cm.
I) A fórmula do Teorema de Pitágoras é a² = b² + c², onde a é a hipotenusa e b e c são os catetos. II) A fórmula do Teorema de Pitágoras é a² = b² + c², onde a é a hipotenusa e b e c são os catetos, mas pode ser alterada para b² = a² + c² ou c² = b² + a² sem modificar o resultado do cálculo. III) Se um triângulo retângulo tem catetos de medidas b = 7,5 cm e c = 10 cm, o valor da hipotenusa é a = 12,5 cm. IV) Se um triângulo retângulo tem catetos de medidas b = 7,5 cm e c = 10 cm, o valor da hipotenusa é a = 17,5 cm.