2. Questões de Concurso

Filtrar

Questões por página:

Do alto de um prédio de 16 metros de altura, um pedreiro esticou uma corda que estava presa ao chão por uma colega, a uma distância de 12 metros da base do prédio, conforme a imagem abaixo. Qual é o comprimento da corda?

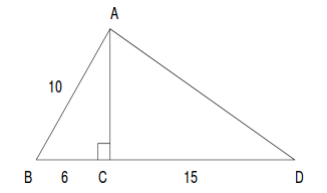
Imagem associada para resolução da questão

Do alto de um prédio de 16 metros de altura, um pedreiro esticou uma corda que estava presa ao chão por uma colega, a uma distância de 12 metros da base do prédio, conforme a imagem abaixo. Qual é o comprimento da corda?

Imagem associada para resolução da questão

Calcule o comprimento de AD na figura abaixo:
Imagem associada para resolução da questão
Em um triângulo retângulo, o complementar de um dos ângulos agudos é o dobro do complementar do outro ângulo agudo.
Logo, o quadrado do cosseno do maior dos ângulos agudos é igual a:
Um poste de 2 m produz uma sombra de 80 cm. A altura de um edifício que no mesmo instante projeta uma sombra de 13 m é
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo