2. Questões de Concurso
  3. Matemática
  4. Assunto - Seno Cosseno e Tangente

Filtrar

Questões por página:

Julgue o item subsequente.


Um farol localizado a 50 metros da costa emite um feixe de luz que incide sobre o topo de uma bandeira hasteada em um mastro na praia. O ângulo de depressão do feixe de luz em relação ao nível horizontal é de 30 graus. A altura do farol é de 30 metros. Determinamos assim que a altura da bandeira hasteada no mastro sera de 35 metros.

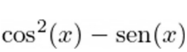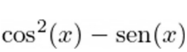Qual o gráfico da função Q34.png (187×52)?
Considere as seguintes afirmações relacionadas aos conceitos de trigonometria:

I. O seno de um ângulo no triângulo retângulo é definido como a razão entre o cateto adjacente e a hipotenusa. II. O cosseno de 90° é igual a zero. III. A tangente do ângulo x é a razão entre o cosseno e o seno de x. IV. O valor de sen(2x) é sempre igual a sen(x)*cos(x) para qualquer x. V. Na geometria euclidiana, a soma dos ângulos internos de um triângulo sempre é igual a 180 graus.

Com base nas afirmações acima, escolha a alternativa correta:
Questão Anulada

Considerando:

 

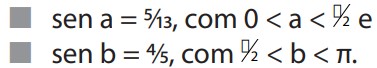
Imagem associada para resolução da questão

 

Então cos(a – b) é:

Um observador está a 20 metros de distância de um prédio.


Desprezando-se a altura do observador e considerando que ele observa o topo do prédio sob um ângulo de 60°, a altura do prédio, em metros, é:

© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo