2. Questões de Concurso

Filtrar

Questões por página:
Considere que a distância, em linha reta, entre Jardim do Seridó e o povoado Santo Antônio (Carnaúba dos Dantas), é 33 km e, entre Brejuí (Currais Novos) e o povoado Santo Antônio, é 44 km, conforme mostra a figura abaixo.

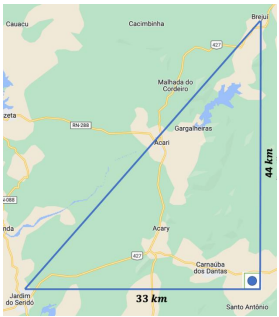
Imagem associada para resolução da questão

Fonte: Modificado de Google Maps.

Considerando, ainda, que as distâncias entre esses três locais compõem um triângulo retângulo, a distância, em linha reta, entre Jardim do Seridó e Brejuí (Currais Novos), corresponde a

No triângulo ABC da figura a seguir, a altura relativa à base BC mede 15 e o raio da circunferência inscrita nele mede 3.


Imagem associada para resolução da questão


Uma circunferência menor é tangente à circunferência inscrita no triângulo ABC e tangente, também, aos lados AB e AC.

O raio dessa circunferência menor mede

Um homem possui um pingente cujo formato é um triângulo equilátero de lado medindo 1 cm. Ele deseja partir esse pingente "ao meio" de modo que sua namorada fique com metade e ele com a outra metade. Então, ele decide traçar uma altura imaginaria e realizar uma quebra, um corte, em cima dessa altura. Dessa forma, qual a medida, em cm, da altura encontrada para que o corte seja feito?
A área de um triângulo equilátero de lado 6 m, é equivalente à área de um quadrado de lado x. O perímetro deste quadrado é igual a:
Um triângulo ABC tem um ângulo de 60 graus e os lados AB e BC medem, respectivamente,6 cm e 8 cm. Qual é a medida do terceiro lado do triângulo?
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo