Questões de Concurso
Filtrar
136 Questões de concurso encontradas
Página 27 de 28
Questões por página:
No projeto, a rampa é a hipotenusa AB do triângulo retângulo ABC. A altura da rampa, representada pelo cateto BC, deverá medir 2 m. A distância AC, representada pelo outro cateto do triângulo, deverá ser tal que a inclinação da rampa, dada pelo ângulo θ no vértice A, não seja superior a 30º.
Nessa situação, sabendo-se que
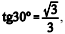o comprimento do cateto AC, em metros, deverá ser tal que O esquema a seguir mostra um observador no ponto O, que representa o cume de uma montanha, e um avião no ponto A, à altura AB do solo. O ponto C, no segmento AB, está a 6 km desse observador.
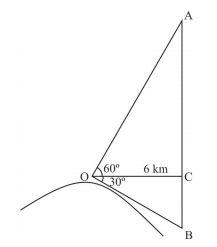
O observador enxerga o avião sob um ângulo de 60° com a horizontal OC e o ponto B, no solo, sob um ângulo de 30° com a mesma horizontal.
Admitindo-se 0,57 e 1,73 como valores aproximados para tg 30° e tg 60°, respectivamente, é correto afirmar que a altura AB do avião é
Em um triângulo retângulo, a hipotenusa mede 13 centímetros e um dos catetos mede 5 centímetros. Nesse triângulo, considere o retângulo inscrito, em que o comprimento do lado maior é igual ao dobro do comprimento do lado menor, e um dos lados maiores está sobre o cateto maior do triângulo.
Com base nessas informações, é correto afirmar que a área desse retângulo é igual a
Ao realizar caminhadas, um atleta quer que sua trajetória forme triângulos equiláteros. Ele inicia no ponto A e percorre três etapas de 15 metros e completa o primeiro triângulo equilátero (ver Figura 1). O atleta continua, na mesma direção e sentido, outros 15 metros e dessa maneira, ele considera que já percorreu o primeiro lado do segundo triângulo equilátero, agora com medida do lado igual a 30 metros (15 + 15, ver na Figura 2). Observe que parte do primeiro lado do segundo triângulo é o mesmo que o terceiro lado do primeiro triângulo. Ele faz mais duas etapas de 30 metros e completa o segundo triângulo equilátero (ver Figura 3).
Para realizar essa caminhada, até agora, o atleta já caminhou 120 metros. Cada vez que completa um novo triângulo equilátero ele continua caminhando mais 15 metros, na mesma direção e sentido, e esse lado fica sendo o primeiro lado do novo triângulo equilátero.
O atleta continua caminhando dessa maneira até completar, exatamente, o sexto triângulo equilátero. A distância total caminhada pelo atleta foi de
Os segmentos CA e MN, na figura, representam respectivamente, uma parede lateral de uma casa e um muro paralelo a essa parede, que ficaram abalados após alguns dias de fortes chuvas. Para evitar um desmoronamento, duas barras de ferro, representadas na figura pelos segmentos AM e CN, foram utilizadas para escorar a parede e o muro.
Sabendo-se que a casa fica em um terreno plano e que as duas barras se interceptam a h metros do solo, pode-se afirmar que o valor de h é
