Questões de Concurso
Filtrar
43 Questões de concurso encontradas
Página 2 de 9
Questões por página:
Questões por página:
Vetores diretores das retas r e s são v = (1,1,2) e w = (1,1,0), respectivamente. Um ponto P ∈ r é (0,1,0) e um ponto Q ∈ s é (0,0,1), logo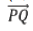
= (0, −1,1). Portanto, a distância entre r e s é:
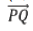= (0, −1,1). Portanto, a distância entre r e s é:
Concurso:
SEE-PE
Disciplina:
Matemática
Julgue o seguinte item, a respeito de determinantes e sistemas lineares.
Considere-se v ∈ ℝn, A ∈ ℝn×n e a matriz M ∈ ℝn×n cujas entradas sejam dadas da seguinte forma: mij =aij, para todo i ∈ {1,2,3, … n, } e j ∈ {1,3,4, …n}, e mi2 = ai2 + vi, i ∈ {1,2,3 ..., n}. Nesse caso, é correto concluir que det(M) = det(A) + |v|, em que |v| =
.
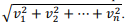Concurso:
SEE-PE
Disciplina:
Matemática
Julgue o seguinte item, a respeito de determinantes e sistemas lineares.
Para que a matriz
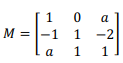
não seja singular, é necessário que a ≠ ± √13/2 - 1/2.
Concurso:
SEE-PE
Disciplina:
Matemática
Julgue o seguinte item, a respeito de determinantes e sistemas lineares.
Considerando-se uma matriz A ∈ ℝm x n, um vetor x ∈ ℝn e b ∈ ℝm, se m < n, então o sistema linear Ax = b nunca terá solução.
Seja T : R2 → R3 uma transformação linear. Sabendo-se que T(1,1) = (1,2,3) e T(1,0) = (1,2,1). Qual das opções a seguir representa T(x, y).
