Concurso:
SEE-PE
Disciplina:
Matemática
Julgue o seguinte item, a respeito de determinantes e sistemas lineares.
Considere-se v ∈ ℝn, A ∈ ℝn×n e a matriz M ∈ ℝn×n cujas entradas sejam dadas da seguinte forma: mij =aij, para todo i ∈ {1,2,3, … n, } e j ∈ {1,3,4, …n}, e mi2 = ai2 + vi, i ∈ {1,2,3 ..., n}. Nesse caso, é correto concluir que det(M) = det(A) + |v|, em que |v| =
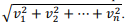 .
.