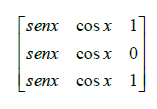Questões de Concurso

Considere a transformação linear f:R2→R3, tal quef(1, 2)=(2, 1, 1) e f(1, −1)=(−1, −2, 1) . Qual é o vetor v ∈ R2 tal que f(v)=(7, 4, 3) ?

Considere os vetores u=(1, 3, −4) e v=(−2, 2, 7) do R3 .

Qual é o valor de m para que o vetor η =(11, 9, m) seja a combinação linear de u e v ?

Considere a matriz A= ⎣⎢⎢⎢⎡​1111​21−12​−231−3​−13−1x​⎦⎥⎥⎥⎤​ .

Qual é o valor de x para que o determinante de A seja igual a zero?

Alice parte da origem O e segue em linha reta por uma distância de a dada em quilômetros (km). Ao chegar ao final desse percurso, ela vira em um ângulo de 45º no sentido horário e anda por mais ra km. Sempre que ela chega ao final de um percurso, ela novamente vira em 45º no sentido horário, e o novo percurso terá comprimento r vezes o último percurso.

A linha poligonal simples na figura abaixo ilustra o passeio de Alice.

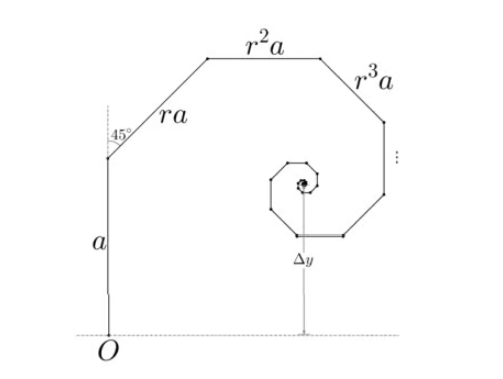
Se Alice mantiver infinitamente esse comportamento, teremos que os comprimentos dos percursos percorridos formam uma progressão geométrica infinita de razão r e termo inicial a . Considerando o problema como ilustrado na figura acima, chamaremos a medida Δy de deslocamento vertical.

Sob as condições descritas acima e considerando que a=1 km e r=21?, qual é o valor do deslocamento vertical?

O determinante associado à matriz quadrada é igual a