Questões de Concurso
Filtrar
329 Questões de concurso encontradas
Página 20 de 66
Questões por página:
Questões por página:
Disciplina:
Matemática
Seja 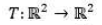 um operador linear tal que, para todo
um operador linear tal que, para todo 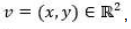 o segmento de reta que liga
o segmento de reta que liga 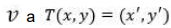 é vertical e tem seu ponto médio sobre a reta
é vertical e tem seu ponto médio sobre a reta 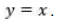 A alternativa que contém a expressão CORRETA do operador linear é:
A alternativa que contém a expressão CORRETA do operador linear é:
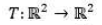 um operador linear tal que, para todo
um operador linear tal que, para todo 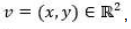 o segmento de reta que liga
o segmento de reta que liga 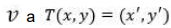 é vertical e tem seu ponto médio sobre a reta
é vertical e tem seu ponto médio sobre a reta 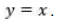 A alternativa que contém a expressão CORRETA do operador linear é:
A alternativa que contém a expressão CORRETA do operador linear é:
Disciplina:
Matemática
Seja 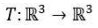 a rotação de um ângulo
a rotação de um ângulo 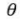 em torno do eixo
em torno do eixo 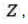 no sentido anti-horário, cuja matriz, em relação à base canônica do
no sentido anti-horário, cuja matriz, em relação à base canônica do 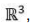 é dada por
é dada por  Considerando o ângulo
Considerando o ângulo 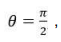 a respeito de
a respeito de 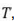 é CORRETO afirmar:
é CORRETO afirmar:
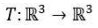 a rotação de um ângulo
a rotação de um ângulo 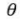 em torno do eixo
em torno do eixo 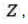 no sentido anti-horário, cuja matriz, em relação à base canônica do
no sentido anti-horário, cuja matriz, em relação à base canônica do 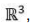 é dada por
é dada por  Considerando o ângulo
Considerando o ângulo 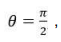 a respeito de
a respeito de 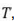 é CORRETO afirmar:
é CORRETO afirmar: Sobre a propriedade de determinante de matrizes, é correto afirmar que:
Marque a alternativa que apresenta a sentença correta sobre as propriedades de matrizes transpostas e inversas.