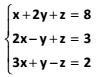Questões de Concurso
Filtrar
266 Questões de concurso encontradas
Página 32 de 54
Questões por página:
Questões por página:
Considerando a matriz A representada abaixo, calcule o determinante da matriz inversa de A.
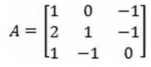
Concurso:
CBM-RO
Disciplina:
Matemática
Uma matriz quadrada A de ordem n é simétrica, se for igual a sua matriz transposta At . Sabendo que a matriz A abaixo é simétrica, determine o valor de m.

Seja a matriz M = (aij)3x3 com 
Determine o valor de det M-1.

Determine o valor de det M-1.
Para que valor(es) de k o sistema abaixo admite uma única solução? 

Concurso:
CBM-RN
Disciplina:
Matemática
O sistema de equações a seguir tem como soma das raízes: