Questões de Concurso
Filtrar
333 Questões de concurso encontradas
Página 5 de 67
Questões por página:
Questões por página:
Concurso:
Prefeitura de João Pessoa - PB
Disciplina:
Matemática
Em um estacionamento de uma loja, há um total de 50 vagas disponíveis para carros e motos. Considerando que todas essas vagas estão ocupadas, resultando em um total de 152 pneus, sem incluir os estepes. A quantidade de motos presentes no estacionamento é de:
Concurso:
Prefeitura de São Caetano do Sul - SP
Disciplina:
Matemática
Sobre a matriz resultante da operação abaixo, podemos afirmar que: 

Concurso:
Prefeitura de Várzea Alegre - CE
Disciplina:
Matemática
A solução do sistema é:
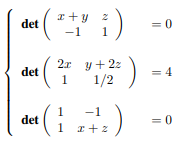
Concurso:
Prefeitura de Várzea Alegre - CE
Disciplina:
Matemática
Sejam V1?, V2?e V3? vértices de um triângulo retângulo em V1?. Suponha que seus catetos possuem medidas l. Considere (aij?)3×3? uma matriz onde aij? é a distância entre os vértices Vi? e Vj?. O determinante de (aij?)3×3? é:
Concurso:
Prefeitura de Itapoá - SC
Disciplina:
Matemática
Analise a equação matricial a seguir:

Um possível valor de p para que a equação tenha solução inteira está na alternativa:

Um possível valor de p para que a equação tenha solução inteira está na alternativa: