Questões de Concurso

Em uma carteira, há R$ 1.570,00 em notas de 20 reais e 50 reais. Sabendo-se que existem 9 notas de 50 reais a mais do que as de 20 reais, qual é o número total de notas existentes na carteira?

As variáveis Y e Y representam, respectivamente, o nível de ansiedade e a nota obtida na prova, dos alunos de uma determinada turma de cálculo. Para estimar valor de Y em função de X, optou-se por utilizar o modelo de regressão linear entre X e Y. A equação utilizada para prever o valor de Y foi determinada como sendo Y = 90,868 -0,2921X, obtida pelo método de mínimos quadrados. Para ajudar a avaliar a qualidade do modelo, o pesquisador decidiu fazer uso do coeficiente de correlação (R) e do coeficiente de explicação (R² ).

Considerando que ambos coeficientes (R e R² ) são diferentes de zero, é CORRETO apenas o que se afirma em:

Em uma fila para atendimento, encontram-se 1.000 pessoas. Em ordem cronológica, cada pessoa recebe uma senha para atendimento numerada de 1 a 1.000. Para a estimação do tempo médio de espera na fila, registram-se os tempos de espera das pessoas cujas senhas são números múltiplos de 10, ou seja,10,20,30,40, ...,1.000.

Considerando que o coeficiente de correlação dos tempos de espera entre uma pessoa e outra nessa fila seja igual a 0,1, e que o desvio padrão populacional dos tempos de espera seja igual a 10 minutos, julgue o item que se segue.

Se a correlação linear for nula, a variância da média amostral será superior a 2 min².

No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 =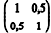 em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

Se representa o modelo ajustado, então Var( ) = Var(g) = σ² × I, em que I é uma matriz identidade e σ² representa a variância dos erros aleatórios.

No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 =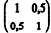 em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

Se a variância de cada erro aleatório fosse igual a 4, as variâncias dos estimadores dos coeficientes do modelo seriam iguais a 2.