2. Questões de Concurso

Filtrar

Questões por página:
A solução da equação complexa |z| − z − 1 − 4i = 0 é:
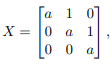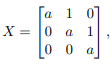Seja X uma matriz quadrada de ordem 3 com entradas reais. As matrizes que comutam com X são todas as matrizes A = (aij ) de ordem 3 com entradas reais tais que AX = XA. Em particular, se 1.png (111×66)com a ∈ R e a ≠ 0, é correto afirmar:

Atribua o valor lógico verdadeiro (V) ou falso (F) às proposições abaixo:


I) 13 é primo e 16 não é um quadrado perfeito.


II) 70 = 7 ou √x2 = |x|


III) O conjunto solução da equação x2 − 4 = 0 é {−2,0} se, e somente se,91 for um número primo.


IV) Se 64 é um cubo perfeito então √2304 = 48.


V) 0 (zero) é par e ímpar simultaneamente.


Agora, a sequência correta (de I a V, nessa ordem) é:

A circunferência de equação x2 + y2 − 14x − 6y + 42 = 0 tem centro C(a, b) e raio r. Então a2 − b2 + r vale:
Sabendo-se que x + 2y = 7, qual o maior valor possível para o produto xy? ( x e y números reais).
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo