Questões de Concurso
Filtrar
127 Questões de concurso encontradas
Página 7 de 26
Questões por página:
Questões por página:
Para a estimação de uma proporção p por meio de amostragem aleatória simples (com reposição) de tamanho n = 100, considere que o estimador dessa proporção seja
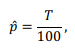
em que T representa uma soma de valores 1 (sucessos) ou 0 (fracassos). Se a estimativa da variância de for igual a 0,0025, então será igual a
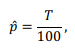
em que T representa uma soma de valores 1 (sucessos) ou 0 (fracassos). Se a estimativa da variância de for igual a 0,0025, então será igual a
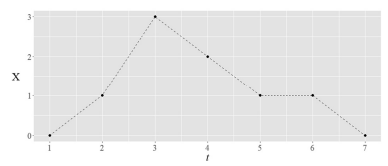
Conforme a figura precedente, que mostra os valores da variável X obtidos em uma amostra de tamanho n = 7, tem-se que a moda de X é igual a
Concurso:
PC-RO
Disciplina:
Estatística
Determinado presídio, que possui 500 celas, será objeto de um levantamento para se estimar a proporção p de detentos que são portadores de certa doença. O levantamento seguirá o seguinte plano amostral: (a) 10 celas serão sorteadas por amostragem aleatória simples; (b) todos os detentos encontrados nessas 10 celas sorteadas serão testados clinicamente para a contagem do número de portadores da doença em questão nesse levantamento.
Considerando-se a situação hipotética apresentada, é correto afirmar que o plano amostral em tela para a estimação da proporção p representa uma
Considerando-se a situação hipotética apresentada, é correto afirmar que o plano amostral em tela para a estimação da proporção p representa uma
Concurso:
PC-BA
Disciplina:
Estatística
Sobre a técnica de amostragem estratificada, assinale o item correto.
As amostras, quanto à forma de seleção, podem ser do tipo probabilístico ou não probabilístico. Como exemplos dessas últimas, podem ser citados os casos de amostras obtidas por cotas, por conveniência ou em bola de neve.
Sobre essas três modalidades, e nessa ordem, é correto afirmar que: