Questões de Concurso
Filtrar
3.799 Questões de concurso encontradas
Página 579 de 760
Questões por página:
Questões por página:
Considere as seguintes afirmações:
( 1 ) 0,999... = 1.
( 2 ) se a/b = c/d, então a /b = a + c / b + d .
( 4 ) 0,1234567891011... é um número racional.
( 8 )  = 26 = 64.
= 26 = 64.
( 16 ) 
O somatório dos itens verdadeiros é igual a:
Seja X = 1,5323232... um número decimal periódico no qual os dígitos 3 e 2 se repetem indefinidamente nesta ordem. Quando X é escrito como uma fração irredutível, o numerador excede o denominador de:
No contexto da Aritmética, a divisão de um valor não nulo por zero é considerada indefinida. Abaixo seguem alguns argumentos, utilizando os números naturais, apresentados por um professor a seus alunos, para demonstrar que essa divisão seria indefinida:
I. Ao se dividir objetos entre pessoas, como se atribuir algo a nenhuma pessoa? Por exemplo, ao se dividir seis doces entre duas crianças cada uma receberia três doces; quantos doces seriam dados a cada pessoa se não houvesse nenhuma pessoa? II. A divisão por zero iria fazer com que falsas igualdades fossem criadas. Por exemplo,2 · 0 = 3 · 0. Se dividirmos ambos os lados por zero, teríamos 2 =3. III. A divisão com resto pode ser considerada como uma sequência de subtrações: subtrai-se o divisor do dividendo sucessivas vezes até atingir um número menor que o divisor. Por exemplo, ao dividir 7 por 3, subtraímos 3 duas vezes de 7 até chegar em 1; assim o quociente é 2 e o resto é 1. Se subtrairmos zero, nunca seria atingido um número menor que o divisor.
Porém, parte destes argumentos pode levar, erroneamente, à conclusão que ao se dividir um número qualquer não nulo por zero também resultaria em zero. Assinale a alternativa que indica quais destes argumentos podem levar a esta conclusão equivocada.
I. Ao se dividir objetos entre pessoas, como se atribuir algo a nenhuma pessoa? Por exemplo, ao se dividir seis doces entre duas crianças cada uma receberia três doces; quantos doces seriam dados a cada pessoa se não houvesse nenhuma pessoa? II. A divisão por zero iria fazer com que falsas igualdades fossem criadas. Por exemplo,2 · 0 = 3 · 0. Se dividirmos ambos os lados por zero, teríamos 2 =3. III. A divisão com resto pode ser considerada como uma sequência de subtrações: subtrai-se o divisor do dividendo sucessivas vezes até atingir um número menor que o divisor. Por exemplo, ao dividir 7 por 3, subtraímos 3 duas vezes de 7 até chegar em 1; assim o quociente é 2 e o resto é 1. Se subtrairmos zero, nunca seria atingido um número menor que o divisor.
Porém, parte destes argumentos pode levar, erroneamente, à conclusão que ao se dividir um número qualquer não nulo por zero também resultaria em zero. Assinale a alternativa que indica quais destes argumentos podem levar a esta conclusão equivocada.
Considere as expressões abaixo:
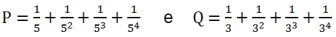
A relação aproximada entre os valores de P e Q é:
Ao longo de um mês, o preço inicial P de um produto passou pelas seguintes alterações (sempre em relação ao preço imediatamente anterior): - Aumento de 20%. - Redução de 15%. - Aumento de 10%.
Assinale a alternativa que indica o preço final do produto em relação ao inicial P:
Assinale a alternativa que indica o preço final do produto em relação ao inicial P: