Questões de Concurso

Se chover hoje à noite, Maria não vai sair. Se não sair, a probabilidade de pedir uma pizza para entrega em casa é de 0,80. Por outro lado, se não chover Maria vai sair, e, nesse caso, a probabilidade de ir a uma pizzaria e pedir uma pizza para consumo no local é de 0,20. Sabendo que a probabilidade de chover hoje à noite é de 0,25, a probabilidade de Maria pedir uma pizza é de:

A função densidade de probabilidade f(t) = 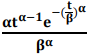t > 0, e α, β > 0 corresponde ao tempo até falhar de um equipamento eletrônico e corresponde à distribuição Weibull com parâmetros α e β. Essa distribuição é usada no dimensionamento do tempo de garantia de um produto eletrônico a ser adquirido por uma instituição judiciária. Então, a diretoria da instituição quer saber da equipe técnica a probabilidade de o equipamento falhar dentro do prazo de 1 ano. A equipe técnica pesquisa o banco de dados da rede de assistência técnica do fabricante do equipamento e, com os dados registrados do tempo de falha do produto, estima os parâmetros α e β em 2 e 5. Dessa forma, é correto afirmar que a probabilidade de falha dentro do prazo de 1 ano é

Considere E1 e E2 dois eventos aleatórios associados a um experimento, supondo que P(E1) = 0,4 enquanto P(E1UE2) = 0,8 e P(E2) = p, então, o valor de p para que E1 e E2 sejam mutuamente exclusivos e o valor de p para que E1 e E2 sejam independentes são, respectivamente,

Um cientista de dados está utilizando SHapley Additive exPlanations (SHAP) para entender a importância das variáveis em um modelo de aprendizado de máquina que prevê a probabilidade de um cliente deixar de ser assinante de um serviço (churn). Considere o seguinte conjunto de dados simplificado com três características para um cliente específico:



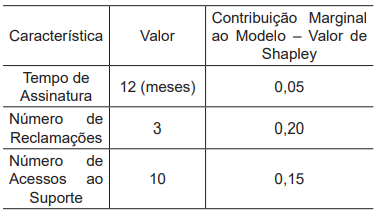
A previsão base do modelo, que representa a probabilidade estimada de um cliente se tornar um churn quando nenhuma das características individuais é considerada, é de 0,30.
Considerando-se esse contexto, qual é a probabilidade prevista pelo modelo para que esse cliente deixe de assinar o serviço?