Questões de Concurso
Filtrar
447 Questões de concurso encontradas
Página 48 de 90
Questões por página:
Questões por página:
Concurso:
TCE-PA
Disciplina:
Estatística
mostrar texto associado
O valor esperado da média amostral é igual a 10.
Concurso:
TCE-PA
Disciplina:
Estatística
mostrar texto associado
A estatística  segue uma distribuição quiquadrado com 1 grau de liberdade.
segue uma distribuição quiquadrado com 1 grau de liberdade.
Concurso:
TCE-PA
Disciplina:
Estatística
Concurso:
TCE-PA
Disciplina:
Estatística
mostrar texto associado
A média amostral segue uma distribuição t de Student com n - 1 graus de liberdade.
Concurso:
TCE-PA
Disciplina:
Estatística
mostrar texto associado
A variância de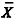 é igual a 100.
é igual a 100.

