Questões de Concurso
Filtrar
26 Questões de concurso encontradas
Página 3 de 6
Questões por página:
Questões por página:
Concurso:
AL-RO
Disciplina:
Estatística
Avalie se as afirmativas a seguir, relacionadas à estimação por máxima verossimilhança de um parâmetro θ, são falsas (F) ou verdadeiras (V).
( ) A função de verossimilhança de um conjunto de variáveis aleatórias é definida como a função de densidade (ou de probabilidade) conjunta dessas variáveis olhada como função de θ.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade uniforme no intervalo (0, θ), o estimador de máxima verossimilhança de θ é máx{Xi}, ou seja, é a n-ésima estatística de ordem.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade N(µ, σ2 ), σ conhecida, o estimador de máxima verossimilhança de µ é a média amostral.
Na ordem apresentada, as afirmativas são, respectivamente,
Concurso:
AL-RO
Disciplina:
Estatística
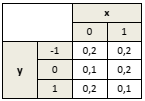
mostrar texto associado
O coeficiente de correlação de X e Y é, aproximadamente, igual a
Concurso:
AL-RO
Disciplina:
Estatística
mostrar texto associado
O valor da constante k é
Concurso:
TCE-PA
Disciplina:
Estatística
Considere que Y seja uma variável aleatória geométrica que representa o número de erros cometidos por um atendente no preenchimento de formulários e que a função de probabilidade de Y seja definida por P(Y = k) = 0,9 × (0,1)k, em que k = 0,1,2, ... A partir dessas informações, julgue o item que se segue.
P(Y ≥ 2) = 0,01.
P(Y ≥ 2) = 0,01.
Concurso:
TCE-PA
Disciplina:
Estatística
Considere que Y seja uma variável aleatória geométrica que representa o número de erros cometidos por um atendente no preenchimento de formulários e que a função de probabilidade de Y seja definida por P(Y = k) = 0,9 × (0,1)k, em que k = 0,1,2, ... A partir dessas informações, julgue o item que se segue.
A variável Y segue uma distribuição com assimetria negativa.
A variável Y segue uma distribuição com assimetria negativa.