Questões de Concurso
Filtrar
946 Questões de concurso encontradas
Página 113 de 190
Questões por página:
Questões por página:
Concurso:
Prefeitura de Conceição de Macabu - RJ
Disciplina:
Matemática
mostrar texto associado
Quantos dias após o início do acompanhamento o número de bactérias presentes nessa cultura era de 1.620?
Concurso:
Prefeitura de Conceição de Macabu - RJ
Disciplina:
Matemática
O gráfico abaixo representa uma função do primeiro grau na forma f(x) = ax + b, onde a e b

Analisando esse gráfico, os coeficientes a e b são, respectivamente:
Concurso:
Prefeitura de Guarapari - ES - 2020
Disciplina:
Matemática
Um determinado elemento químico radioativo se decompõe de acordo com a função P(t) = P0x 3 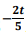 , onde P0 representa a massa inicial da substância, em gramas, e P(t) representa a massa final da substância, t horas após o início da observação. Após quantas horas do início da observação, a massa da substância se reduziu à nona parte?
, onde P0 representa a massa inicial da substância, em gramas, e P(t) representa a massa final da substância, t horas após o início da observação. Após quantas horas do início da observação, a massa da substância se reduziu à nona parte?
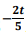 , onde P0 representa a massa inicial da substância, em gramas, e P(t) representa a massa final da substância, t horas após o início da observação. Após quantas horas do início da observação, a massa da substância se reduziu à nona parte?
, onde P0 representa a massa inicial da substância, em gramas, e P(t) representa a massa final da substância, t horas após o início da observação. Após quantas horas do início da observação, a massa da substância se reduziu à nona parte? Ao acrescentar 20 unidades à terça parte de um número, o resultado é 45. Assinale a alternativa que representa esse número.
Uma caixa de som e duas mesas foram adquiridas pela quantia de R$ 10.400,00. O custo da caixa de som ultrapassou em R$ 7.600,00 o das duas mesas. Sabendo-se, ainda, que o preço de uma das mesas é igual ao da outra mais R$ 200,00, assinale a alternativa que indica CORRETAMENTE o valor da caixa de som.