Questões de Concurso
Filtrar
738 Questões de concurso encontradas
Página 68 de 148
Questões por página:
Questões por página:
Disciplina:
Matemática
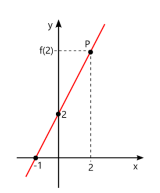
O gráfico abaixo representa a função do primeiro grau ƒ(x) = αx + b , com α ≠ 0 e {α, b} ⊂ ?. A distância do ponto P até a origem (0,0) é igual a:
Disciplina:
Matemática
A equação geral da reta que passa pelos pontos A e B, sendo considerado a função ƒ(x) = 2x, é igual a:

Concurso:
Prefeitura Municipal de Rio Claro - SP
Disciplina:
Matemática
João tem o dobro de figurinhas do que possui Carlos. Carlos tem 40 figurinhas a menos do que Felipe. Felipe tem dois terços do total de figurinhas que João e Carlos possuem juntos. O número total de figurinhas que esses três meninos possuem é
Disciplina:
Matemática
Ao imprimir uma equação do 2º grau, Henrique notou que o coeficiente do termo x² saiu borrado e ilegível, como mostra a figura.

Sabendo que uma das soluções da equação era – 3, Henrique conseguiu descobrir corretamente o valor do coeficiente que saiu borrado e calculou a outra solução da equação, que era

Sabendo que uma das soluções da equação era – 3, Henrique conseguiu descobrir corretamente o valor do coeficiente que saiu borrado e calculou a outra solução da equação, que era
Concurso:
Prefeitura Municipal de Harmonia - RS
Disciplina:
Matemática
A solução S que satisfaz a equação logarítmica log(x−3)(2x 2 − 14x + 24) = 2 é dada pelo conjunto: