2. Questões de Concurso

Filtrar

Questões por página:
Analise as afirmativas a seguir, marque V para as verdadeiras e F para as falsas.

( ) Para a função f : N → N definida por f(x) ݂= x + 1 o conjunto imagem é tal que Im(f) = N*

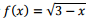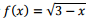( ) O domínio da função f : R → R definida por Imagem associada para resolução da questão é tal que D(f) = { x ∈ R | x < 3}

( ) Dada a função f : R → R definida por f(x) = x2 - 4x + 4 , seu domínio é tal que D(f ) = R

A sequência está correta em
A diferença entre os logaritmos de dois número, X e Y, na base 2 é 5. Sabendo que a soma de X e Y é 99 e que X > Y, então, na equação log(x–66)T = Y – 1, T é igual a:
Joana foi ao mercado e comprou as seguintes quantidades dos seguintes produtos:

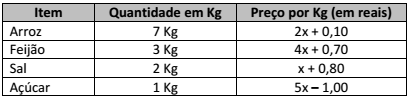
Imagem associada para resolução da questão

Sabendo que ela pagou um total de R$ 43,00 na compra, então o preço de 1 Kg de açúcar é:


O lucro de certa empresa, em reais, é dado pela função f(x) = –5 x2 + 600x + 5.000, onde x é o número de meses de existência da empresa. Sabendo que a empresa fechou após 20 meses de quando teve seu maior lucro, então o lucro que essa empresa obteve no seu último mês de existência foi:

As funções exponenciais são muito usadas para modelar o crescimento ou o decaimento populacional de uma determinada região em um determinado período de tempo. A função P(t) = 234(1,023)t modela o comportamento de uma determinada cidade quanto ao seu crescimento populacional em um determinado período de tempo, em que P é a população em milhares de habitantes e t é o número de anos desde 1980.

Qual a taxa média de crescimento populacional anual dessa cidade?

© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo