2. Questões de Concurso
  3. Estatística
  4. Assunto - Inferência estatística

Filtrar

Questões por página:
No período de um ano, uma indústria teve 50 acidentes. A área de segurança no trabalho da indústria imagina se o dia da semana é um fator influente no número de acidentes. Com base nos dados coletados, dispostos na tabela abaixo (Tabela 3), foram feitas diversas suposições. Uma delas está errada.

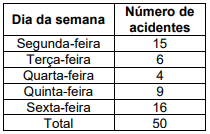
Imagem associada para resolução da questão

Tabela 3

A esse respeito, analise as afirmativas abaixo e dê valores Verdadeiro (V) ou Falso (F).
( ) Como hipótese nula num eventual teste de hipóteses a se realizar, pode-se supor que o dia da semana não influencia a quantidade de acidentes, isto é, todos os dias são igualmente prováveis.
( ) Na situação descrita pode ser aplicado um teste de aderência χ2 (Qui-quadrado).
( ) Aplicado um teste de aderência χ2, os resultados obtidos foram: χ2crítico = 9,49 e χ2teste = 11,4. Dessa maneira, podemos concluir que ocorrem mais acidentes às sextas-feiras.
( ) Aplicado um teste de aderência χ2, cuja hipótese nula foi de que os dias são igualmente prováveis, contra a alternativa de que não o são, os resultados obtidos foram: χ2crítico= 9,49 e χ2teste =11,4 . Dessa maneira, podemos concluir que não se pode aceitar que os dias sejam igualmente prováveis.
Assinale a alternativa que apresenta a sequência correta de cima para baixo.
Se uma moeda é honesta, espera-se que em 50% das vezes em que ela é lançada apareça cara. Uma moeda foi lançada 50 vezes, e em 20 apareceu cara. Usando nível de significância de 1%, podemos afirmar que:(use a Tabela 2 abaixo na solução da questão).

Tabela da distribuição normal padronizada – P(0≤Z≤z)

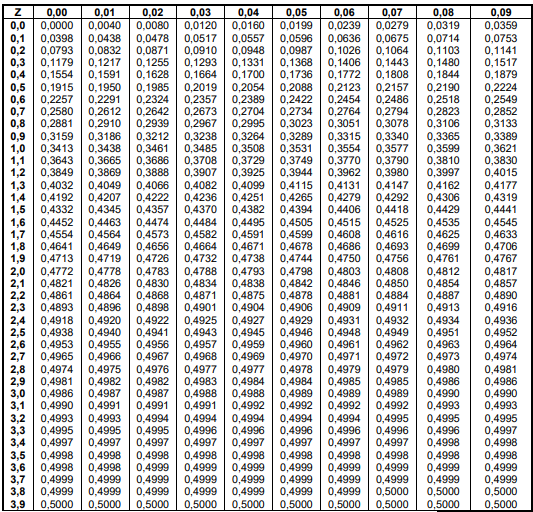
Imagem associada para resolução da questão


Tabela 2 Fonte: Stevenson, W.J.1986. Estatística aplicada à administração. São Paulo, Harbra, p.461.

Três grupos de pacientes, de 5 indivíduos cada, foram submetidos a três tratamentos distintos para dor: analgésico A, analgésico B e placebo. Mediu-se o tempo (em unidades de tempo) que os pacientes relataram a ausência da dor, para efeito de comparação entre os tratamentos. Os resultados estão na tabela 2 abaixo:

Imagem associada para resolução da questão

 Tabela 2

O teste anova (α = 0,05), aplicado aos dados, forneceu estatística F teste = 2,60 e valor F crítico = 3,89. Diante do exposto, podemos afirmar que:

Questão Anulada
Um fabricante de cerveja pretende construir um intervalo de 90% de confiança para o conteúdo médio das latas. Se o desvio padrão do conteúdo é de 15 ml e o erro não deve ultrapassar 2 ml, assinale a alternativa que apresenta o tamanho de amostra que o fabricante deve utilizar.

A Tabela 1 deve ser utilizada na solução da questão.

Tabela da distribuição normal padronizada – P(0≤Z≤z)

Imagem associada para resolução da questão


Tabela 1 Fonte: Stevenson, W.J.1986. Estatística aplicada à administração. São Paulo, Harbra, p.461

Um estudo tem o objetivo de verificar se existe independência entre tipos de crimes e regiões de um país. A seguinte Tabela de Contingência mostra os números observados em uma amostra aleatória de tamanho n = 789 casos registrados nas regiões.


Imagem associada para resolução da questão


Sabe-se que Imagem associada para resolução da questão = 27,91 e P(Imagem associada para resolução da questão > 27,91) = 0,0000. Então, é correto afirmar que as frequências esperadas das células (C1, R2) e (C3, R1), o valor-p e a decisão quanto à relação entre Tipo de Crime e Região, do teste da hipótese de independência entre Tipo de Crime e Região, serão:





© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo