Questões de Concurso

Ao analisar uma amostra aleatória simples composta de 324 elementos, um pesquisador obteve, para os parâmetros média amostral e variância amostral, os valores 175 e 81, respectivamente.

Nesse caso, um intervalo de 95% de confiança de μ é dado por

De acordo com o texto 7A3-I, o estimador não viesado 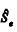da variância residual é

Uma fábrica de cerveja artesanal possui uma máquina para envasamento regulada para encher garrafas de 800 mL. Esse mesmo valor é utilizado como média µ, com desvio padrão fixo no valor de 40 mL. Com o objetivo de manter um padrão elevado de qualidade, periodicamente, é retirada da produção uma amostra de 25 garrafas para se verificar se o volume envazado está controlado, ou seja, com média µ = 800 mL. Para os testes, fixa-se o nível de significância α = 1%, o que dá valores críticos de z de - 2,58 e 2,58.

Com base nessas informações, julgue os seguintes itens.

II Caso uma amostra apresente média de 778 mL, os técnicos poderão parar a produção para a realização de nova regulagem, pois tal valor está dentro da região crítica para o teste.

III A produção não precisaria ser paralisada caso uma amostra apresentasse média de 815 mL, pois este valor está fora da região crítica para o teste.

Assinale a opção correta.

Uma equipe de engenheiros da qualidade, com vistas a estimar vida útil de determinado equipamento, utilizou uma amostra contendo 225 unidades e obteve uma média de 1.200 horas de duração, com desvio padrão de 150 horas.

Considerando-se, para um nível de confiança de 95%, z = 1,96, é correto afirmar que a verdadeira duração média do equipamento, em horas, estará em um intervalo entre

Um estimador que fornece a resposta correta em média é chamado não enviesado. Formalmente, um estimador é não enviesado caso seu valor esperado seja igual ao parâmetro que está sendo estimado.

Os possíveis estimadores para a média populacional (µ) incluem β, média de uma amostra, α, a menor observação da amostra, e π, a primeira observação coletada de uma amostra. Considerando essas informações, julgue os itens subsequentes.

I A média de uma amostra (β) é exemplo de um estimador enviesado para a média populacional (µ), pois seu valor esperado é igual à média populacional, ou seja, E(β) = µ.

II A menor observação da amostra (α) é um exemplo de estimador não enviesado, pois o valor da menor observação da amostra deve ser inferior à média da amostra; portanto, E(α) < µ.

III A primeira observação coletada de uma amostra equivale a tomar ao acaso uma amostra aleatória da população de tamanho igual a um e, portanto, é considerado um estimador não enviesado.

Assinale a opção correta.