Questões de Concurso
Filtrar
31 Questões de concurso encontradas
Página 5 de 7
Questões por página:
Questões por página:
No item a seguir, é apresentada uma situação hipotética, seguida de uma assertiva a ser julgada, a respeito de máximos e mínimos de funções, da regra de trapézio para cálculo aproximado de integrais e de análise combinatória.
Uma caixa, sem tampa superior, deve ter a forma de um paralelepípedo reto-retângulo, de base quadrada e volume igual a 4.000 cm3 . A espessura do material a ser utilizado para a confecção dessa caixa é desprezível. Nesse caso, para a confecção da caixa com as referidas especificações, serão necessários, pelo menos,1.200 cm2 de material.
Uma caixa, sem tampa superior, deve ter a forma de um paralelepípedo reto-retângulo, de base quadrada e volume igual a 4.000 cm3 . A espessura do material a ser utilizado para a confecção dessa caixa é desprezível. Nesse caso, para a confecção da caixa com as referidas especificações, serão necessários, pelo menos,1.200 cm2 de material.
Julgue os próximos itens, relativos à função f(x, y) = 4 + cos(x + y), para (x, y) restritos ao domínio 0 ≤ x ≤ 2π e 0 ≤ y ≤ 2π.
O volume de um sólido compreendido entre o gráfico da função z = f(x, y) e o plano xOy é inferior a 144 unidades de volume.
O volume de um sólido compreendido entre o gráfico da função z = f(x, y) e o plano xOy é inferior a 144 unidades de volume.
Questão Anulada
Dada a função aceleração α(t)= 6t + 2 , marque a opção que representa a respectiva função posição, s(t) sabendo-se que a velocidade em t = 0 é 0 e a posição em t = 0 é 1.
A integral 
x cos(x) dx vale
Considerando‐se o gráfico de y = f(x) para –2 ≤ x ≤ 2 apresentado acima, os valores de a e b que minimizam a integral
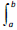f (x) dx são, respectivamente, 