Questões de Concurso
Filtrar
125 Questões de concurso encontradas
Página 2 de 25
Questões por página:
Questões por página:
Um aluno perguntou a seu professor de Matemática se o determinante da matriz M, a seguir, é igual a zero.

Sem efetuar os cálculos, o professor afirmou que sim, pois:

Sem efetuar os cálculos, o professor afirmou que sim, pois:
Concurso:
Prefeitura de Cubati - PB
Disciplina:
Matemática
Considere as matrizes abaixo:
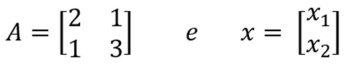
A forma quadrática associada à matriz A é dada por Q(x) = xT Ax onde xT é a transposta do vetor x. Calcule Q(x) e escolha a alternativa correta.
Concurso:
Prefeitura de Balneário Camboriú - SC
Disciplina:
Matemática
Considere o sistema abaixo:

O valor de a para que esse sistema tenha infinitas soluções é:
Concurso:
Prefeitura de Padre Bernardo - GO
Disciplina:
Matemática
Considere a função real a seguir.
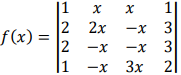
Então,
Concurso:
Prefeitura de Camocim de São Félix - PE
Disciplina:
Matemática
Certo atleta participou de um torneio, em que foram realizadas nove provas, três a cada dia. Considere que a matriz a seguir representa a nota obtida por esse atleta em cada prova, com i representando o dia e j representando a ordem da prova.
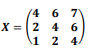
Sabendo-se que a média desse atleta corresponde ao determinante da matriz X, qual média foi obtida por ele nesse torneio?
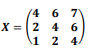
Sabendo-se que a média desse atleta corresponde ao determinante da matriz X, qual média foi obtida por ele nesse torneio?