Questões de Concurso
Filtrar
141 Questões de concurso encontradas
Página 22 de 29
Questões por página:
Questões por página:
Um criador de cães observou que as rações das marcas A, B, C e D contêm diferentes quantidades de três nutrientes, medidos em miligramas por quilograma, como indicado na primeira matriz abaixo. O criador decidiu misturar os quatro tipos de ração para proporcionar um alimento adequado para seus cães. A segunda matriz abaixo dá os percentuais de cada tipo de ração nessa mistura.

Quantos miligramas do nutriente 2 estão presentes em um quilograma da mistura de rações?

Quantos miligramas do nutriente 2 estão presentes em um quilograma da mistura de rações?
Concurso:
PM-MT
Disciplina:
Matemática
mostrar texto associado
Os valores de x para os quais a matriz A admite inversa são:
Concurso:
PM-MS
Disciplina:
Matemática
Considere as matrizes A = 
O determinante do produto A B é um número:
Concurso:
PM-MS
Disciplina:
Matemática
mostrar texto associado
Das afirmações acima:
Concurso:
PM-ES
Disciplina:
Matemática
Para saber o custo total (em reais) na produção de x uniformes para um grupo de soldados, primeiramente substitui-se cada elemento x, da matriz a seguir, pela quantidade de uniformes que se quer produzir e calcula-se o determinante dessa matriz, obtendo-se, assim, o custo total na produção destes x uniformes igual ao valor do determinante.
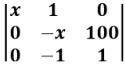
Dessa forma, para se produzir 70 uniformes para um grupo de soldados, o custo total nessa produção será de
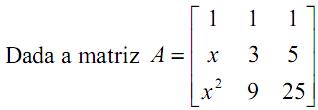

 cujo produto (executado na ordem conveniente) resultará em uma matriz C = (C
cujo produto (executado na ordem conveniente) resultará em uma matriz C = (C